Matematické Fórum

frantax · 29. 06. 2013 18:03

Ahoj, resim integral viz nize chci se zeptat jak zjistim kolik se rovná B, A jsem spocital.
Dekuji.

$\int_{1}^{\sqrt{3}}\frac{x+2}{x(x^2+1)}$

$A(x^2+1)+Bx=x+2$

$x=0; A*1=2;A=2$

jelena · 29. 06. 2013 18:19

Zdravím,

asi úvodní rozklad na parciální zlomky nebude v pořádku - jak jsi rozložil? Děkuji.

Jinak - pokud jsi dosazoval x=0 a vypočetl A, potom můžeš dosazovat nalezené A a další x z def. oboru. Ovšem zde ještě nezafunguje, protože rozklad má být jinak - tak až opravíš rozklad.

frantax

↑ jelena:
hoj, delal jsem to takhle

$\frac{A}{x}+\frac{B}{x^2+1}$

jelena · 29. 06. 2013 18:29

↑ frantax:

to jsi dělal jen částečně dobře - ${x^2+1}$ nemá kořeny v R, tedy čitatel tohoto zlomku má být jinak - máterály máš?

frantax

↑ jelena:↑ jelena:

Ahoj, podle toho co mam v sesite to nejspis bude Bx+C
_____
x^2+1

$A(x^2+1)+Bx^2+cx=x+2$

Ale ted nevim co mam dat misto x aby me neco vyslo.:(

bismarck · 29. 06. 2013 19:48

↑ frantax:

$\int_{1}^{\sqrt{3}}\frac{x+2}{x(x^2+1)}dx$

$\frac{x+2}{x(x^2+1)}=\frac{1}{x^{2}+1}+\frac{2}{x(x^{2}+1)}=\frac{1}{x^{2}+1}+\frac{Ax}{x^{2}+1}+\frac{B}{x}$

$\frac{2}{x(x^{2}+1)}=\frac{Ax}{x^{2}+1}+\frac{B}{x}$
Dopočítaj A, B

frantax · 29. 06. 2013 20:09

↑ bismarck:
No tak me vyslo B=2 A=-1

takhle ?

bismarck · 29. 06. 2013 20:19

↑ frantax:

B=2 - správne
A=-1 - nesprávne

frantax · 29. 06. 2013 20:22

↑ bismarck:

tak to B sem vypocital tak ze sem dal X=0 no a teda to A mam vypocitat prosim jak ?
jinak ja sem tam dal to B=2 a za x dal 1..

bismarck

$\frac{2}{x(x^{2}+1)}=\frac{Ax}{x^{2}+1}+\frac{B}{x}$

$\frac{2}{x(x^{2}+1)}=\frac{Ax}{x^{2}+1}+\frac{B}{x}\\ \frac{2}{x(x^{2}+1)}=\frac{Ax^{2}+B(x^{2}+1)}{x(x^{2}+1)}\\ 2=Ax^{2}+Bx^{2}+B\\ 2=B+x^{2}(A+B)$

$B=2\\ A+B=0$

A=-2
B=2

Stačí len dopočítať
$\int_{1}^{\sqrt{3}}\frac{x+2}{x(x^2+1)}dx= \int_{1}^{\sqrt{3}}\frac{1}{x^{2}+1}-\frac{2x}{x^{2}+1}+\frac{2}{x}dx=...$

frantax · 29. 06. 2013 20:38

↑ bismarck:
Aha, tka to asi nechapu od zacatku, kde se tam vzala nahore ta dvojka..ja to delal takhle

$\frac{Ax}{x^2+1}+\frac{B}{x}=\frac{x+2}{x(x^2+1)}$

bismarck · 29. 06. 2013 20:40

↑ frantax:

$\frac{x+2}{x(x^2+1)}=\frac{x}{x(x^2+1)}+\frac{2}{x(x^2+1)}=\frac{1}{(x^2+1)}+\frac{2}{x(x^2+1)}=...$

frantax · 29. 06. 2013 20:49

↑ bismarck:

AHa,ale jak k tomu dojdu ? nerozumim tomu proc se to zrovna dela tak, kdyz budu mit nejaky priklad, jak poznam ze to mam takhle delat.

jelena · 29. 06. 2013 21:29

↑ frantax:

Kolega ↑ bismarck: (viz jeho jiné příspěvky) je zdatný a zkušený počtář - tedy již ze zápisu původního zlomku vidí možné úpravy, co zjednoduší další výpočty.

V prvním kroku podělil čitatel jmenovatelem člen po členu, v dalším kroku využil, že část zlomků již koeficienty má a hledal pouze koeficienty pro porovnání zlomků: $\frac{2}{x(x^{2}+1)}=\frac{Ax}{x^{2}+1}+\frac{B}{x}$ .

Pokud není to přesně vidět, používej Tvou univerzální metodu rozkladu z příspěvku 5: $A(x^2+1)+Bx^2+Cx=x+2$

Zde jsou možnosti takové:

a) můžeš dosadit 3 různé hodnoty x a vyřešit vzniklé soustavy rovnic (neznámé A, B, C)
b) porovnat koeficienty u stejných mocnin x (pro tuto metodu je třeba výraz nalevo ještě upravit a stejné mocniny seskupit k sobě).

Podrobně je všechno zde. Ještě se podívej po tématu - zdá se, že kolega Bismarck příspěvky editoval, aby bylo více srozumitelné. Všechno v pořádku? Děkuji.

frantax · 29. 06. 2013 21:47

↑ jelena:
Ahoj, muzu se zeptat jak to bude vypadat kdyz by se to delal tou moji univerzalni metodou?, jak vypoctu abc, kdyz je nemuzu vynulovat pomoci x=0 , tak jak jsem vypocital ze A=2.

jelena · 29. 06. 2013 21:55

↑ frantax:

To jsem napsala - viz 2. část příspěvku:

Zde jsou možnosti takové:

a) můžeš dosadit 3 různé hodnoty x a vyřešit vzniklé soustavy rovnic (neznámé A, B, C)
b) porovnat koeficienty u stejných mocnin x (pro tuto metodu je třeba výraz nalevo ještě upravit a stejné mocniny seskupit k sobě).

$A(x^2+1)+Bx^2+Cx=x+2$

dosazováním x=0 máš A=2
dosazováním x=1, A=2 a x=-1, A=2 máš soustavy:
$4+B+C=3$
$4+B-C=1$

---------------------------------
nebo seskupením:
$Ax^2+A+Bx^2+Cx=x+2$
$x^2(A+B)+xC+A=x+2$
porovnávám koeficienty u stejných mocnin:

$A+B=0$ (protože napravo není x^2)
$C=1$
$A=2$

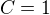
je všemu rozumět?

frantax · 29. 06. 2013 22:13

↑ jelena:
diky, tou soustavou rovnic me to vyslo, ale pomoci toho porovnavani mocnin asi moc nechapu..

A=2 zjistim ze: x^2 *(A+B)

C=1 ze: xC

Ale nechapu to A+B=0

Diky .

jelena · 29. 06. 2013 23:30

↑ frantax:

metoda porovnání koeficientů u stejných mocnin je určitě popsána ve všech metodách rozkladů na parciální zlomky (a plyne z pravidel rovnosti polynomů) - v odkazu bylo? ↑ příspěvek 14:.

Levou a pravou stranu uspořádaš tak, abys stejné mocniny x viděl:

po úpravě máme: $x^2(A+B)+xC+A=x+2$ "doplním" (domyslím) stejné mocniny nalevo a napravo:

$(A+B)x^2+Cx^1+Ax^0=0\cdot x^2+1\cdot x+2\cdot x^0$

tak je vidět, které koeficienty budeme porovnávat?

frantax · 30. 06. 2013 09:49

↑ jelena:

tak ted uz ano. diky

jelena · 30. 06. 2013 09:56

↑ frantax:

také děkuji.

Matematické Fórum

#1 29. 06. 2013 18:03

Integrál

#2 29. 06. 2013 18:19

Re: Integrál

#3 29. 06. 2013 18:25 — Editoval frantax (29. 06. 2013 18:27)

Re: Integrál

#4 29. 06. 2013 18:29

Re: Integrál

#5 29. 06. 2013 19:21 — Editoval frantax (29. 06. 2013 19:28)

Re: Integrál

#6 29. 06. 2013 19:48

Re: Integrál

#7 29. 06. 2013 20:09

Re: Integrál

#8 29. 06. 2013 20:19

Re: Integrál

#9 29. 06. 2013 20:22

Re: Integrál

#10 29. 06. 2013 20:23 — Editoval bismarck (29. 06. 2013 20:37)

Re: Integrál

#11 29. 06. 2013 20:38

Re: Integrál

#12 29. 06. 2013 20:40

Re: Integrál

#13 29. 06. 2013 20:49

Re: Integrál

#14 29. 06. 2013 21:29

Re: Integrál

#15 29. 06. 2013 21:47

Re: Integrál

#16 29. 06. 2013 21:55

Re: Integrál

#17 29. 06. 2013 22:13

Re: Integrál

#18 29. 06. 2013 23:30

Re: Integrál

#19 30. 06. 2013 09:49

Re: Integrál

#20 30. 06. 2013 09:56

Re: Integrál

Zápatí