Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » absolutní hodnota komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 07. 2013 13:08 — Editoval kryštof (01. 07. 2013 21:43)
absolutní hodnota komplexního čísla
Ahoj, mám takovýhle problém: Dokažte, že pro každá dvě  platí
platí  . Zkusil jsem to, ale nevím, jestli je to dobře.
. Zkusil jsem to, ale nevím, jestli je to dobře.
Je  ,
,  , pak
, pak 
 a předpokládáme, že nerovnost
a předpokládáme, že nerovnost  platí. Levá i pravá strana nerovnice je větší nule, takže ji můžeme umocnit
platí. Levá i pravá strana nerovnice je větší nule, takže ji můžeme umocnit



levá strana  je vždycky větší nule, takže
je vždycky větší nule, takže
1.) 
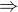
 platí
platí 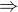 platí i
platí i 
2.)  , takže l. i p. strana
, takže l. i p. strana  jsou obě větší než nula a nerovnici můžeme umocnit
jsou obě větší než nula a nerovnici můžeme umocnit




 , což platí pro všechna reálná a,b,x,y
, což platí pro všechna reálná a,b,x,y 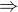 platí
platí 
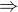 platí i
platí i  .
.
Co myslíte?
Offline
- (téma jako vyřešené označil(a) kryštof)
#2 01. 07. 2013 15:42
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: absolutní hodnota komplexního čísla
Jo to vypada správne, hezké.
Offline
#3 01. 07. 2013 15:46
Re: absolutní hodnota komplexního čísla
↑ kryštof:
Ahoj.
předpokládáme, že nerovnost
platí.
To nemůžeš předpokládat, když to máš dokazovat (to by se to dokazovalo, pokud bychom dokazované tvrzení předpokládali :-) ) .
Offline
#4 01. 07. 2013 20:21 — Editoval kryštof (01. 07. 2013 20:44)
Re: absolutní hodnota komplexního čísla
↑ Rumburak:
Proč ne?? Když z toho předpokladu vyvodíme výrok, o kterém víme, že platí, pak je to snad totéž, jako kdybychom postupovali obráceně, a z pravdivého výroku vyvodili to, že platí i dokazované tvrzení (alespoň v tomhle případě)? Prosím, vysvětli mi to.
Offline
#5 01. 07. 2013 21:22 — Editoval vanok (02. 07. 2013 06:21)
Re: absolutní hodnota komplexního čísla
Poznamka: z malymy upravamy ( a doplnkamy) mozes redigovat tvoj dokaz vo forme ekvivalencii.
To povoli vdaka strukture dokazu ti dat dobru konkluziu.
V tvojej redakcii si vlastne dokazal, ze A implikuje B... Ale to este neznamena vseobecne, ze B implikuje A.
Ako vyriesit tvoj problem:
1) ukazat ze ide o ekvivalenciu , ako som to uz vyssie napisal.
Alebo
2) zacat tvoj dokaz od B a prist k A.
Pravidlo je: B plati, B implikuje A, potom A.
Cize ako vidime poznamka kolegu ↑ Rumburak: je uplne spravna.
Inac je velmi dolezita poznamka, tvoj symbol  pouzivats ako skratku a to je v protiklade z tym, ze ide matematicky slovny text. Take symboly su povolene len v formalnom vyjadreni. .. I ked na strednej skole niektori ucitelia pouzivaju taketo miesanini, co je skoda.
pouzivats ako skratku a to je v protiklade z tym, ze ide matematicky slovny text. Take symboly su povolene len v formalnom vyjadreni. .. I ked na strednej skole niektori ucitelia pouzivaju taketo miesanini, co je skoda.
Nakoniec tato vlasnost ma aj ine dokazy. Mozno si aj na internete take najdes.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 01. 07. 2013 21:26 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Skoda ze duplicity sa nedaju zmazat
#7 01. 07. 2013 22:22 — Editoval kryštof (01. 07. 2013 22:30)
Re: absolutní hodnota komplexního čísla
Pro všechna reálná čísla a,b,x,y platí





 (protože |ax+by|>=(ax+by) )
(protože |ax+by|>=(ax+by) ) (protože levá i pravá strana jsou větší nebo rovny nulepro všechna a,b,x,y, můžeme to odmocnit)
(protože levá i pravá strana jsou větší nebo rovny nulepro všechna a,b,x,y, můžeme to odmocnit)
takže  pro všechna
pro všechna  ,
,  .
.
Když teda budu postupovat takhle, tak je to správně, že?
Offline
#8 01. 07. 2013 23:00 — Editoval vanok (01. 07. 2013 23:04)
Re: absolutní hodnota komplexního čísla
Minimalne pridaj aspon toto:
Ale na zaciatok napis, ze vlasnosti kazde ho vyssie ho riadku implikuje vlasnosti nasledujuceho.
Po piatej a osmej vlasnosti pridaj aspon to, ze je to vdaka tomu ze funkcia  je rastuca.
je rastuca.
Inac, po malych opravach, je to dobre napisany dokaz.
A ake metody poznas este na dokaz tejto vlasnosti?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 02. 07. 2013 07:12
Re: absolutní hodnota komplexního čísla
↑ kryštof:
a nejde to nejak jednoduse pres vektory?
neco jako
no a protoze cos nalezi <-1,1>
pak musi platit
podobne, jako se ve fyzice pracuje s cislama. Uhly fi1, fi2 a fi=fi2-fi1 znat pro dukaz netreba.
Offline
#12 02. 07. 2013 09:42
Re: absolutní hodnota komplexního čísla
↑ mmch:
Dokaz ↑ kryštof: ma vyhodu ze pouziva sredoskolske pojmy.
Je to mozne dokazat napr aj vdaka pojmu REALNA CAST komplexneho cisla; alebo aj vdaka uhlu vektorov co representuju complexne cisla 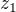 a
a  .
.
A iste vela foristov zaujima tvoj dokaz, tak ho nam tu napis tak dokonale ako to urobil nas kolega [re]p375620|kryštof[/re.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 02. 07. 2013 10:04 — Editoval Rumburak (02. 07. 2013 10:12)
Re: absolutní hodnota komplexního čísla
↑ kryštof:
Ahoj.
Chceme-li dokázat platnost výroku  , pak začít předpokladem, že výrok
, pak začít předpokladem, že výrok  PLATÍ, je nesprávné PRINCIPIÁLNĚ, protože
PLATÍ, je nesprávné PRINCIPIÁLNĚ, protože
v tom případě už by nebylo potřeba výrok  dokazovat (když podle předpokladu beztak platí) . Takovýmto způsopbem
dokazovat (když podle předpokladu beztak platí) . Takovýmto způsopbem
by se dal triviálně "dokázat" úplně každý výrok.
Po vysvětlení, které Ti napsal kolega ↑ vanok:, Ti to možná už je jasné.
Zmiňme se ještě o možnosti dokázat platnost nějakého výroku  sporem: zde bychom předpokládali, že výrok
sporem: zde bychom předpokládali, že výrok  NEPLATÍ,
NEPLATÍ,
a snažili bychom se z tohoto předpokladu odvodit nějaký výrok zjevně napravdivý (tedy výrok, který by byl "ve sporu s pravdou").
Offline
#14 02. 07. 2013 10:19
Re: absolutní hodnota komplexního čísla
↑ vanok:
secist silu F1+F2=F se uci snad jeste na ZS.
vektorovy pocet se uci na SS
v cem je problem?
Ja povazuju uvahu k dukazu za kompletni. Nebo vidis chybu?
hele - do skoly to nikdo nepotrebujem tak prosimte po me nechtej abych to psala stylem Necht je dano .... atd
Offline
#15 02. 07. 2013 11:46
Re: absolutní hodnota komplexního čísla
↑ mmch:
Ahoj.
Mám za to, že kolega ↑ vanok: Ti chtěl říci, že je škoda, že Tvoje myšlenka není vyjádřena natolik podrobně,
aby byla srozumitelná pro potřebného čtenáře (takového, který neumí provést důkaz samostatně).
Jestli to rozvedeš do větších podrobností nebo ne, je samozřejmě Tvoje věc.
Ještě poznámka: Ony ustálené matematické formulace, které se používají v učebnicích, mají svůj smysl v tom, že jsou
přesné a není možno v nich nechtěně nalézat nějaké jinotaje, které by si každý vykládal jinak.
Offline
#16 02. 07. 2013 11:52
Re: absolutní hodnota komplexního čísla
↑ mmch:
Vidim ze bezny stredoskolak by tomu bez kompletneho vysvetlenia nemohol rozumiet.
No mozno nemas chut sa z tym hrat a ho napisat pre kolegov co su stredoskolaci.
A inac dnesne programy v CZ, SK na ZS a SS nepoznam.....ale mat definiciu z rychlika neznamena vediet pouzivat pojmy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 02. 07. 2013 11:55
Re: absolutní hodnota komplexního čísla
Pozdravujem ↑ Rumburak:, pisali sme spolu a vidim, ze nase nazory v podstate su tie iste.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 02. 07. 2013 14:22
Re: absolutní hodnota komplexního čísla
Necht jsou dána komplexní čísla 

Nechť pro komplexní číslo z 
platí 
Všechna tři komplexní čísla zaneseme v komplexní (Gaussově) rovině. Viz obrázek. Sčítání vektorů je známo z analytické geometrie nebo z fyziky (viz rozklad sil).
Využijeme znalosti ze základní školy a zjistíme, že z obrázku plyne:
Povšimněte si prosím střídavých úhlů, jsou vyznačené oranžově. Druhý zásadní úhel pro důkaz je vyznačen červeně.
Také připomínám, že velikost vektoru je jeho absolutní hodnota.
A teď zásadní úvaha. Víme, že funkce cosinus má obor hodnot <-1,1> , proto platí

a proto musí platit:
CBD
tož mládenci, doufám, že to oceníte, stálo mě to hodinu boje s pipláním se obrázku a jeho odesíláním ;-)
Offline
#20 02. 07. 2013 16:32
Re: absolutní hodnota komplexního čísla
↑ mmch:
To už je lepší. Na SŠ škole by to patrně prošlo, ale na matfyzu už ne, protože v důkazu je odvolávka na obrázek, což není korektní
(z VŠ matematiky jsou známy příklady dokládající, že odvolávat se na obrázek může vést k omylům).
Zkusme Tvoji ideu zpracovat bez obrázku. Máme tedy
 ,
,

 .
.
Předpokládejme, že  . Musí proto platit
. Musí proto platit  (reálná část součtu se rovná součtu reálných částí) ,
(reálná část součtu se rovná součtu reálných částí) ,  (imaginární část součtu se rovná součtu imaginárních částí).
(imaginární část součtu se rovná součtu imaginárních částí).
Poslední dvě rovnice umocníme na druhou a sečteme. Dostaneme .
.
Tuto rovnost upravíme na
(1)  ,
,
k tomu použito
 ,
,
 .
.
Z (1) plyne nerovnost
(2)  ,
,
protože  a
a  . Nerovnost (2) zapíšeme ve tvaru
. Nerovnost (2) zapíšeme ve tvaru , odtud odmocněním
, odtud odmocněním  , tj.
, tj.  .
.
Offline
#21 02. 07. 2013 17:09
Re: absolutní hodnota komplexního čísla
↑ Rumburak:
jo, tak to je presne to, cemu jsem se chtela vyhnout. Silene pocitani. Davam prednost elegantnim uvaham.
jinak gratuluju k matfyzu ;-)
Offline
#23 02. 07. 2013 21:32 — Editoval vanok (03. 07. 2013 11:35)
Re: absolutní hodnota komplexního čísla
↑ kryštof:, mozno sa ti ine demonstracie ako ta tvoja budu pacit. Ale ver mi ta tvoja ma pre teba najvadciu hodnotu a mozes byt hrdy, ze si ju skoro sam urobil.
A co toto? (bez obrazku, ale na ilustaciu ho doporucujem urobit)
Nech  a
a  rovinne vektory, representuju komlexne cisla
rovinne vektory, representuju komlexne cisla  .
.
Ak ich uhol je  , tak ich skalarny sucin je
, tak ich skalarny sucin je  , kde
, kde  su dlzky vektorov
su dlzky vektorov  a
a  .
.
Akoze ![kopírovat do textarea $cos(\varphi) \in [-1; +1]$](/mathtex/34/3464ad981e4e40696c6af21f40593d4f.gif) , mame
, mame 

Akoze dufam, ze dobre poznate vlasnosti skalarneho sucinu necham vam to dokoncit... ( no ale, ak treba, nevahajte napisat vase otazky)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » absolutní hodnota komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)