Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 07. 2013 22:52
Stanovení taylorova rozvoje funkce
Dobrý den.
Mám příklad. Stanovte Taylorův rozvoj funkce 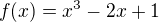 v bodě
v bodě 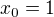 (3. stupně).
(3. stupně).
Vím, že 1. derivace je: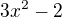 , druhá derivace
, druhá derivace  a třetí derivace
a třetí derivace  . Jinak už nevím, co s tím, protože to nemůžu najít nikde pořádně vysvětlené.
. Jinak už nevím, co s tím, protože to nemůžu najít nikde pořádně vysvětlené.
Offline
#2 07. 07. 2013 01:52 — Editoval user (07. 07. 2013 01:53)
Re: Stanovení taylorova rozvoje funkce
Zdravím,
v prvé řadě je dobré si uvědomit, že Taylorův rozvoj (n-tého stupně) polynomu n-tého stupně bude ten samý polynom, pouze jinak zapsaný (pokud má být ve středovém tvaru), jinak není třeba nic počítat a zadání příkladu je rovnou i výsledek.
V zadání ho zřejmě chtějí ve středovém tvaru.
Teď jsou 2 možnosti.
Zaprvé využít toho, že se jedná o stejný polynom a stačí pouze vyřešit rovnici  vzhledem k
vzhledem k  .
.
Druhý postup, který jsi zvolil je použitelný pro libovolnou funkci a vychází z definice Taylorova polynomu. Stačí tedy, Tebou spočtené derivace vyčíslit v bodě 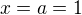 a dosadit do prvního vzorce zde.
a dosadit do prvního vzorce zde.
Offline
#3 07. 07. 2013 02:25
Re: Stanovení taylorova rozvoje funkce
ahoj ↑ Fobl:,
za podmienok co iste poznas viez ze Taylor-ov rozvoj sa pise
v pripade polynomu tretieho stupna ( ktory splna vsetki podmienky pre jeho existenciu )
jeho rozvoj od tretieho stupna jednoznacne urceny a bude vzdy polynom tretieho stupna z nulovym zvyskom.
Akoze tento rozvoj je vzdy jednoznacne urceny, mozes k nemu prist presne ako si zacal... podla vzorca co som vysie pripomenul.
poznamka: ak by si k tomu rozvoju prisiel aj inou metodou, tak ci tak by si dostal, pochopitelne,l ten isty rozvoj.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 08. 07. 2013 08:35
Re: Stanovení taylorova rozvoje funkce
↑ Fobl:
Zdravím kolegu z FAVu :)
V tomto případě se jedná o zobrazení polynomu na polynom. Ve zkoušce můžeš pro dobrý pocit předvést výpočet Taylorova polynomu pomocí derivací, to není tak složité a vzorec se dá zapamatovat. A v tomto případě je chyba rovna nule, což je logické a není to potřeba dokazovat, stačí pouze říci, že se jedná právě o zobrazení z polynomu na polynom. Protože pokud vhodně upravíš výsledek roznásobením závorek, dostaneš zpátky původní fci.
PS. : Před dvěma lety jsem také absolvoval zkoušku z MA1 a byli tam také jen a pouze polynomy jako funkce pro Taylora...
Offline
#5 09. 07. 2013 17:33
Re: Stanovení taylorova rozvoje funkce
Dobrý den.
Zkusil jsem dosadit do Taylorova vzorce, ale nevím jestli to je dobře.
0. derivace 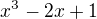 po dosazení za
po dosazení za 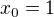 mi vyjde 0,
mi vyjde 0,
1. derivace 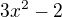 po dosazení za
po dosazení za 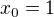 mi vyjde 1,
mi vyjde 1,
2. derivace  po dosazení za
po dosazení za 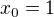 mi vyjde 6 a
mi vyjde 6 a
3. derivace je 6.
Po dosazení do Taylorova vzorce mi vyjde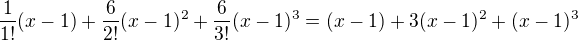
Offline
#7 09. 07. 2013 20:10 — Editoval vanok (10. 07. 2013 14:56)
Re: Stanovení taylorova rozvoje funkce
Poznamka: na skuske nezabudni povedat, ze tento rozvoj od radu 3 ma nulovy zvysok.
Cize ide o specialny pripad, ked sa rozvoj identicky rovna danej funkcii.H
A preto aj ked to sokne urcitych ludi, mozes vdaka tomu co sme tu popisali, bez akokolveho vypoctu, povedat, ze Taylorov rozvoj okolo 1, striktne vyssieho radu ako 2, je dany polynom.
( nie je vobec podstatne ci ho nejako rozvinies alebo nie)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
