Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rucni vypocet autokorelace - seriova nezavislost slozek
#1 16. 07. 2013 11:41
Rucni vypocet autokorelace - seriova nezavislost slozek
Zdravim,
mel bych dotaz na zpusob rucniho vypoctu autokorelace. Jedna se o oblast odhadu klasického lineárního regresního modelu, napr. 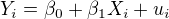 . Dle jednoho z Gauss-Markovovych předpokladu musi platit
. Dle jednoho z Gauss-Markovovych předpokladu musi platit 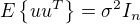 , kde
, kde  je sloupcovy vektor obsahujici
je sloupcovy vektor obsahujici  hodnot nepozorovatelne nahodne slozky modelu a
hodnot nepozorovatelne nahodne slozky modelu a 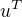 je radkovy vektor techto hodnot.
je radkovy vektor techto hodnot.
Kovariancni matice nahodnych slozek by tedy mela byt rovna 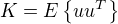 =
= .
.
Obecne vsak vyjde matice jako  .
.
Protoze me zajima autokorelace 1. radu, tak jednotlive prvky kovariancni matice spocitam podle definice 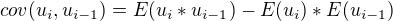 .
.
A prave zde narazim na problem a nevim, jak dal. 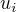 a
a 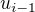 nejsou vektory jako u "bezne kovariance dvou nahodnych velicin L a M"(tu umim spocitat), ale konkretni realna cisla. Stredni hodnota
nejsou vektory jako u "bezne kovariance dvou nahodnych velicin L a M"(tu umim spocitat), ale konkretni realna cisla. Stredni hodnota 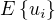 je (podle mne) vlastne stredni hodnota z jednoho konkretniho cisla, tedy
je (podle mne) vlastne stredni hodnota z jednoho konkretniho cisla, tedy 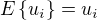 , podobne
, podobne 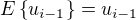 . Vyraz
. Vyraz 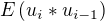 nevim jak spocitat vubec, protoze podle definice kovariance nahodnych velicin L a M plati
nevim jak spocitat vubec, protoze podle definice kovariance nahodnych velicin L a M plati 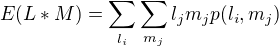 s prislusnymi vyznamy. Pro muj pripad nevim, co mam za jednotlive promenne zde dosadit, kdyz zadne pravdepodobnosti vlastne nemam k dispozici.
s prislusnymi vyznamy. Pro muj pripad nevim, co mam za jednotlive promenne zde dosadit, kdyz zadne pravdepodobnosti vlastne nemam k dispozici.
Ma otazka tedy je, jak rucne spocitam matici 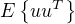 , pokud mi bude zadany konkretni vektor
, pokud mi bude zadany konkretni vektor  , napr.
, napr. 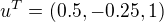 ? Pokud neco o autokorelaci vygoooglim, tak se to temer vzdy resi v nejakem softwarovem produktu, ktery uz "vyhodi" nejaky vysledek, podle ktereho se pak uz jen rozhoduje, zda je autokorelace pritomna nebo ne. Nejde mi o to, jak se zjistuje pritomnost autokorelace, ale zajima me konkretni numericky postup vypoctu te matice
? Pokud neco o autokorelaci vygoooglim, tak se to temer vzdy resi v nejakem softwarovem produktu, ktery uz "vyhodi" nejaky vysledek, podle ktereho se pak uz jen rozhoduje, zda je autokorelace pritomna nebo ne. Nejde mi o to, jak se zjistuje pritomnost autokorelace, ale zajima me konkretni numericky postup vypoctu te matice 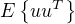 v pripade zadani vektoru
v pripade zadani vektoru  .
.
V zadne ucebnici statistiky jsem nenasel jediny reseny priklad na autokorelaci, tak nevim, jak na to. Nevi nekdo mimochodem o nejakem zdroji s resenymi priklady (i anglickem)? Diky
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rucni vypocet autokorelace - seriova nezavislost slozek
