Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 07. 2013 12:30 — Editoval jelena (30. 07. 2013 12:52)
Nevlastní integrál - konvergence
Dobrý den,
chtél bych se nékoho zeptat, nemůžu přijít na tento příklad:
Dokažte, že 
 konverguje k hodnotě
konverguje k hodnotě  . Nevím si rady s tou absolutní hodnotou.
. Nevím si rady s tou absolutní hodnotou.
Děkuji za nápovědu, popř. náznak postupu jaký mám zvolit.
Stačí pouze dokázat, že 
Děkuji.
Jelena: edit přidávám odkaz na řešení od kolegy martisek. Kolegovi děkuji.
Offline
#2 24. 07. 2013 12:56 — Editoval Bati (24. 07. 2013 20:34)
Re: Nevlastní integrál - konvergence
Dobrý den,
arkustangens je lichá funkce, tudíž absolutní hodnota z něj je funkce sudá. Proto ten integrál je stejný jako 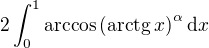 . Snadno se ověří, že
. Snadno se ověří, že ![kopírovat do textarea $\left(\text{arctg}\: x\right)^{\alpha}\in D(\arccos)=[-1,1]\quad\forall x\in[0,1]\quad\forall\alpha\geq1$](/mathtex/73/73d2dd2c1967d6a136313ff9d0143f00.gif) . Protože funkce v integrálu je složení spojitých funkcí, je sama spojitá na omezeném uzavřeném intervalu a tedy integrál je konvergentní.
. Protože funkce v integrálu je složení spojitých funkcí, je sama spojitá na omezeném uzavřeném intervalu a tedy integrál je konvergentní.
Offline
#3 24. 07. 2013 13:14
Re: Nevlastní integrál - konvergence
Ahoj↑ Bati:,
děkuji za postup.
Ještě poslední otázka: Proč je ten integrál ve tvém postupu vynásobený dvěma?
Proč se integrál zastaví na hodnotě 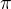 ? Je integrál vlastní?
? Je integrál vlastní?
Děkuji, ale moc tomu nerozumím.
Offline
#4 24. 07. 2013 13:22
Re: Nevlastní integrál - konvergence
↑ Tomas5:
Je vynásobený, protože jsem vzal jen polovinu intervalu, přes který se integruje. A to proto, že daná funkce je sudá. Stejně jako např.  .
.
Netvrdím, že se zastaví na hodnotě pí, ani nevím moc, co tím máš na mysli. Arkustangens je rostoucí, tudíž jeho maximální hodnota v intervalu [0,1] je 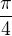 , což je číslo menší než jedna, takže se bude při mocnění jen zmenšovat, pokud je mocnina větší jak jedna.
, což je číslo menší než jedna, takže se bude při mocnění jen zmenšovat, pokud je mocnina větší jak jedna.
Offline
#8 24. 07. 2013 14:19 Příspěvek uživatele Bati byl skryt uživatelem Bati. Důvod: Hloupost
#10 24. 07. 2013 23:39
Re: Nevlastní integrál - konvergence
↑ Tomas5:
Takze chces dokazat neco jako  ? Napada me postup - aproximuj arctg i arccos Taylorovym polynomem, (melo by vyjit
? Napada me postup - aproximuj arctg i arccos Taylorovym polynomem, (melo by vyjit  ), coz dava
), coz dava  . Ted uz staci dokazat, ze
. Ted uz staci dokazat, ze  , coz vypada slibne..
, coz vypada slibne..
Mohlo by to fungovat, je to treba rozepsat (a najit pripadne chyby)..
Offline
#12 25. 07. 2013 01:31
Re: Nevlastní integrál - konvergence
↑ martisek:
No posledni radek by si docela zaslouzil komentar (proc lze prohodit integral a limitu?). Taky myslim, ze posloupnosti fci (a Lebesgueova veta) se neberou v 1. rocniku..
Offline
#13 25. 07. 2013 17:27
Re: Nevlastní integrál - konvergence
Dobré odpoledne,
Z tvého příspěvku jsem zjistil, že to konverguje k pi, ale nerozumím tomu, že  konverguje k nule a ne k
konverguje k nule a ne k  . K nule by to konvergovalo jenom v nule? Prosím o zdůvodnění. Jinak moc děkuji.
. K nule by to konvergovalo jenom v nule? Prosím o zdůvodnění. Jinak moc děkuji.
Poznámka: Posloupnostem funkcí nerozumím (neprobrali jsme je ještě).
Offline
#14 25. 07. 2013 18:30 — Editoval martisek (25. 07. 2013 18:34)
Re: Nevlastní integrál - konvergence
↑ kexixex:
proc lze prohodit integrál a limitu?
Protože integrál je taky limita - limita dolních resp. horních součtů:

↑ Tomas5: :
Nerozumím tomu, že  konverguje k nule a ne k
konverguje k nule a ne k 
V intervalu <-1;1> je  No a co udělá každé číslo
No a co udělá každé číslo  , když ho budeš umocňovat a umocňovat a umocňovat...do nekonečna?
, když ho budeš umocňovat a umocňovat a umocňovat...do nekonečna?
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#15 25. 07. 2013 18:44
Re: Nevlastní integrál - konvergence
↑ martisek:
Tak například , ale
, ale  .
.
Takže je třeba to nějak zdůvodnit (neříkám, že v tomto příkladě to nefunguje).
Offline
#16 25. 07. 2013 18:46
Re: Nevlastní integrál - konvergence
Ahoj,
martisek napsal(a):
V intervalu <-1;1> je
No a co udělá každé číslo
, když ho budeš umocňovat a umocňovat a umocňovat...do nekonečna?
Když budu umocňovat číslo menší než jedna do nekonečna, vyjde v limitě 0.
Offline
#17 25. 07. 2013 19:02
Re: Nevlastní integrál - konvergence
↑ Tomas5:
Když budu umocňovat číslo menší než jedna do nekonečna, vyjde v limitě 0.
Správně. Právě proto jsem napsal (↑ martisek:) :
Posloupnost funkcí  konverguje na intervalu (-1;1) k funkci
konverguje na intervalu (-1;1) k funkci 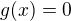
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#18 25. 07. 2013 19:07
Re: Nevlastní integrál - konvergence
↑ Bati:
Pozor!
Není pravda, že
to platí jen pro x>0 !!
Pro x<0 je to 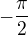 a pro x=0 je to nula.
a pro x=0 je to nula.
Postup v integrálu je možný proto, že ta limita je nula v celém intervalu, přes který se má integrovat.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#19 25. 07. 2013 19:11
Re: Nevlastní integrál - konvergence
↑ martisek:
Samozřejmě, že je myšleno pro x>0, to není ve sporu s ničím a tak jsem to myslel.
Offline
#21 25. 07. 2013 20:06 — Editoval Bati (25. 07. 2013 20:10)
Re: Nevlastní integrál - konvergence
↑ martisek:
Tam jsem se přepsal, nemá tam být  , ale
, ale  , to se omlouvám, jinak si stojím za svým - limita je definována na prstencovém okolí a tu nulu tam dosadit klidně můžu, protože
, to se omlouvám, jinak si stojím za svým - limita je definována na prstencovém okolí a tu nulu tam dosadit klidně můžu, protože  je spojitá fce.
je spojitá fce.
A narážel jsem na to, že obecně nelze jen tak zaměňovat limity, jak už dříve zmínil kexiex. Bez ohledu na tento příklad s integrálem.
Offline
#22 25. 07. 2013 21:49
Re: Nevlastní integrál - konvergence
↑ Bati:
1) tu nulu tam dosadit klidně můžu...
Jenže s nulou nemůžeš žonglovat, jak se ti to hodí. Počítáš-li s hodnotou x=0 ve výrazu 
musíš s ní počítat i v 
a to pak nemůžeš říct, že ta limita je pi/2.
2) Limity nezaměňuju ani "obecně", ani "jen tak". Využívám prostě a jednoduše větu
U limit integrálů, pokud existují, je totiž úplně jedno, zda "zvenku" zjemňuješ dělení a "venvitř" zvedáš alfa (první limita), nebo naopak "zvenku" zvedáš alfa a "venvitř" zjemňuješ dělení (druhá limita), anebo to zcela libovolně kombinuješ (třetí limia).
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#23 25. 07. 2013 22:13
Re: Nevlastní integrál - konvergence
↑ martisek:
No podle vety jeste teda v postupu zbyva overit predpoklady, takze napriklad (mimo jine) ukazat, ze existuje  a cemu se rovna...
a cemu se rovna...
Offline
#24 25. 07. 2013 22:31
Re: Nevlastní integrál - konvergence
↑ kexixex:
To je sice pravda, ale to bych sem musel dost tupě opsat cca tři stránky známé z Riemannova integrálu - zjemňování dělení, horní a dolní součty atd. v nepatrné modifikaci kvůli tomu alfa. A to tedy opravdu dělat nebudu...
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#25 25. 07. 2013 22:47
Re: Nevlastní integrál - konvergence
↑ martisek:
Dobrý večer, mně postačí vysvětlení z příspěvku č.11. Moc mi to pomohlo, ale jak se to dá vyřešit pomocí metod prvního ročníku (např. řad, Taylorova polynomu) atd. ? Myslm si, že tohle je příliš pokročilé...
↑ Bati:
Díky za postup.
Offline