Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 07. 2013 19:37
Nezávislost grafu
Ahoj,
pomohli byste mi prosím najít nezávislé množiny v následujích grafech (resp. nějak jednoduše osvětlili postup)? Vím, že nezávislá množina grafu = žádné 2 body nejsou spojeny hranou.
Na obr. níže jsou zakroužkované body patřící do nezávislých množin. 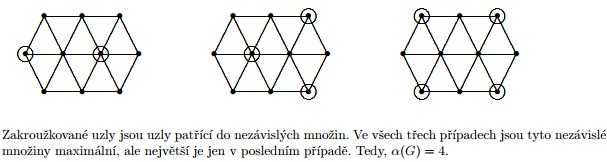
Offline
#2 26. 07. 2013 22:13 — Editoval ondrej.hav (26. 07. 2013 22:38)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Nezávislost grafu
Nezávislá množina jako taková je třeba i jeden uzel. Obecně, pokud máš množinu, která je nezávislá a odebereš jeden prvek, dostaneš zase nezávislou množinu. Tudíž má smysl se ptát na maximální nezávislou množinu. To si si ale ve skriptech určitě přečetl.
Najít maximální nezávislou množinu je snadná úloha řešitelná v P. Kdežto najít největší nezávislou množinu je 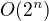
Otázkou je tedy co vlastně chceš najít.
EDIT: Pokud tedy hledáš maximální nezávislou množinu, pak funguje hladový algoritmus. Tedy: Vybereš si (náhodně) jeden uzel, ten přidáš do množiny. Pak postupně procházíš všechny další uzly a pokud můžeš, přidáš ho do množiny. Výsledná množina je samozřejmě maximální. Pokud budeš mít štěstí, může být i největší.
Offline
#3 26. 07. 2013 23:45
Re: Nezávislost grafu
↑ ondrej.hav:
Ok, ale proč je a(g) = 4? Proč jsou na obrázku zakroužkované zrovna tamty body?
Offline
#4 27. 07. 2013 00:45 — Editoval ondrej.hav (27. 07. 2013 00:56)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Nezávislost grafu
↑ Shelber: se značí nezávislost grafu. To je velikost NEJVĚTŠÍ nezávislé množiny. Tedy největší ze všech maximálních.
se značí nezávislost grafu. To je velikost NEJVĚTŠÍ nezávislé množiny. Tedy největší ze všech maximálních.
A proč jsou zakroužkovány zrovna ty uzly, které zakroužkovány jsou? Zakroužkována je na každém grafu maximální nezávislá množina. Jednou má velikost 2, jednou 3 a ta poslední 4. Tenhle graf má ještě jednu největší nezávislou množinu. Tu by si samozřejmě mohl zakroužkovat taky. Ale určitě nemá nezávislou množinu, které by se skládala z pěti uzlů.
EDIT: Rozdíl mezi největší a maximální je jasný? Z toho by mohlo vycházet určité nepochopení. Jinak je to poměrně jasné.
Offline
#5 27. 07. 2013 10:22
Re: Nezávislost grafu
↑ ondrej.hav:
Maximální vs největší chápu (i v těch skriptech je na to kladen důraz), ale stále nechápu tu nezávislou množinu :-(
Mám graf nahoře a chci hledat maximální nezávislou množinu. Použiju teda hladový algoritmus - vyberu nějaký uzel a přidám ho do množiny... tady se ztrácím. Procházím všechny další uzly a pokud MUZU, přidám je do množiny. Jak poznám, kdy můžu? Stále mi nejsou jasné ty pravidla, kdy je daná množina max. nezávislá.
Offline
#6 27. 07. 2013 10:31 — Editoval jarrro (27. 07. 2013 10:35)
Re: Nezávislost grafu
nie som grafar, ale myslím si, že môžeš pridať vtedy keď skúmaný vrchol nie je spojený hranou so žiadnym vrcholom z aktuálnej množiny
podľa tvojich obrázkov je maximálna nezávislá množina taká, že sa k nej už žiadny vrchol pridať nedá bez toho aby bol spojený hranou s nejakým vrcholom z tej množiny
a najväčšia je taká ktorá má navyše ešte viac najviac rovno vrcholov ako každá iná nezávislá množina
myslím si, že táto definícia nevylučuje viac maximálnych množín s rovnakým počtom vrcholov takisto ani viac najväčších množín teda nemusí byť tá množina určená jednoznačne
na tvojom grafe napríklad dvojprvková maximálna je ľubovoľná dvojica nesusedných vrcholov ležiacich na "strednej priečke" a podobne v prípade napríklad úplného grafu je každá jednoprvková množina vrcholov najväčšia snáď som tu nepopísal bludy ak áno upozornite na to niekto
MATH IS THE BEST!!!
Offline
#7 27. 07. 2013 10:49
Re: Nezávislost grafu
Aha, tak to je jednoduchý :-)
Ještě by mě zajímalo to maximální vs největší. Nalezení největší nezávislé množiny je NP-těžký prblém (exponenciální složitost). nalezení maximální nezávislé množiny je polynomiální problém. Proč?
jde o to, že max. nezávislých množin může být v grafu x a počítač by musel porovnat všechny možné kombinace a vybrat největší číslo? Co to znamená, že je NP-těžký? Že když budu mít hodně vstupných dat může výpočet trvat i několik let?
Offline
#8 27. 07. 2013 13:03
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: Nezávislost grafu
NP-težký problém je takový, na který se dá v polynomiálním čase prevést každý problém v NP. Na problém nezávislé množiny mužeš v polynomialním čase prevést každý problém z NP (dúkaz tohohle býva ve skriptech o zložitosti). Takže pokud by si našel polynomialní algoritmus na problém nezávislé množiny, najdes zaroven polynomální algoritmus na každý problém v NP, vrátane obchodního cestujícího, SAT, 3-obarvení atď. A taky by si tím dokázal větu P=NP.
To ze je problem NP-tezky neznamena, ze je v NP! A taky neznamena, ze existuje nan exponencialni algoritmus! Muzes mit NP-tezky problem, ktery je este zlozitejsi a neexistuje pro ani exponencialni algoritmus.
Problém je v NP, pokiaľ sa dá riešiť v polynomiálnom čase na nedeterministickom turingovom stroji.
Problém je v P, pokiaľ sa dá riešiť v polynomiálnom čase na deterministickom turingovom stroji.
Z toho vidieť jasne, že 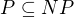 . Ale jestli
. Ale jestli 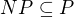 to se uz nevi, ale silne se predpoklada, ze ne.
to se uz nevi, ale silne se predpoklada, ze ne.
Problem je NP-uplny, pokud je NP-tezky a patri do NP. Prakticky se overuje to, jestli problem je v NP pomoci certifikatu. Certifikat, je neco co ti dokaze, ze vysledek ktery mas, je pravdivy.
Problem nezavisle mnoziny je casto formulovan takhle
Existuje v grafu nezavislá množina velkosti k?
Certifikát, který by ukázal, že táto veta je pro graf G pravdivá, je konkrétní nezávislá množina vrcholú. V polynomiálním čase jednoduše zjistím, že tato množina je skutečne nezávislá a že má skutečne velikost k.
Mužu teda říct, že Problem nezavisle množiny patři do NP.
Na kazdy problem v NP urcite existuje exponencialní algoritmus, teda spis algoritmus bezici v case 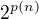 takze v exponentu muze byt i polynom. Pretoze certifikatu je exponencialne mnoho a daji se overit v polynomialnim case.
takze v exponentu muze byt i polynom. Pretoze certifikatu je exponencialne mnoho a daji se overit v polynomialnim case.
To ze je problem  NP-tezky se dokazuje tak, ze najdes nejaky jiny vhodny problem
NP-tezky se dokazuje tak, ze najdes nejaky jiny vhodny problem  o kterem vis, ze je NP-tezky. A dokazes, ze
o kterem vis, ze je NP-tezky. A dokazes, ze  se da prevest v polynomialnim case na
se da prevest v polynomialnim case na  . A tim dokazes, ze i kazdy problem v NP se da prevest v polynomialnim case na
. A tim dokazes, ze i kazdy problem v NP se da prevest v polynomialnim case na  .
.
Offline