Matematické Fórum

To je hodně obecná otázka, zkus, prosím, nějak víc specifikovat co ti není jasné.

↑ Shelber:
Jo takhle. Graf je tedy Ham. pokud v něm existuje Ham kružnice. A 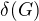je minimální stupeň grafu. Což je nejmenší ze stupňů všech vrcholů.

Takže ta první věta říká, že pokud je každý uzel spojený alespoň s půlkou všech uzlů grafu tak najdeš kružnici, která bude obsahovat všechny uzly.

btw. http://cs.wikipedia.org/wiki/Hamiltonovsk%C3%BD_graf

EDIT Zkus si to zjednodušeně představit tak, že pokud je minimální stupeň všech vrcholů alespoň n/2 tak z každýko uzlu vede alespoň n/2 hran. To je dohromady už takový množství, že z něj musíš vždy být schopen sestavit tu kružnici. Tedy to dolní omezení stupně je vlastně dolní omezení počtu hran v grafu.

d(x) je stupen vrcholu x. Teda kolik hran vychadzi z vrcholu x. Veta 5.3 teda rika, ze pokud soucet stupnu kazdych 2 nesousednych vrcholu je vetsi nebo rovny n, tak G je hamiltonovsky. Vsimni si, ze z toho vyplyva, ze plati veta 5.2. Pokud kazdy vrchol ma stupen aspon n/2, tak urcite soucet stupnu kazdych 2 nesousednych vrcholu je vetsi rovny n a G je hamiltonovsky

↑ Shelber:
Co se týče významu, tak první věta plyne z té druhé. Oreho věta a lemma mají speciální význam, protože na jejich základě můžeme definovat uzávěr grafu.

Pak totiž Bondy+Chvátal říká, že pokud je uzávěrem G úplný graf, pak G je HAM. A důkaz Oreho lemmatu nám dává polynomiální algoritmus k nalezení HAM kružnice.

V obecém případě je HAM NP-C problém.

Říkáš to dobře. Heuristika říká buďto "ANO" nebo "NEVÍM". U Oreho řekne nevím pokud nebude možné sestrojit uzávěr tak aby byl úplným grafem. 

Obecně je HAM v NP-C, ale ty poslední 2 věty jsou divně formulované. Ne-li špatné. Problém jako takový je pořád NP-C. Akorát existují heuristiky, které mohou zafungovat "dobře".

Btw zamysli se, co by znamenalo, že jsi převedl NP-C problém na P?