Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence obecné řady (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 08. 2013 17:48
Konvergence obecné řady
Zdravím,
prosím o pomoc s obecným tvrzením. Ve skriptech není objasněno, takže se asi jedná o nějakou banalitu, která mi přesto uniká.
Mějme obecnou řadu 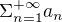 . Označme
. Označme 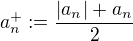 a
a  pro všechna přirozená n. Pak platí
pro všechna přirozená n. Pak platí 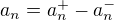 (to je mi ještě jasné). A teď:
(to je mi ještě jasné). A teď:
Když původní řada konverguje absolutně, pak řada  i řada
i řada 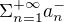 konvergují.
konvergují.
Když původní konverguje neabsolutně, pak řada+ i řada- podstatně divergují.
Není mi jasné, proč to z toho plyne, čím ty implikace podložit.
Děkuju za případné trknutí.
Offline
- (téma jako vyřešené označil(a) Polopat)
#2 05. 08. 2013 18:10 — Editoval Mihulik (05. 08. 2013 18:12)
Re: Konvergence obecné řady
Ahoj,
co třeba elementárně takhle:
Nechť řada  absolutně konverguje.
absolutně konverguje.
Označme  a
a 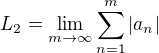
Dle předpokladu 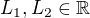 .
.
Potom ale (dle aritmetiky limit) 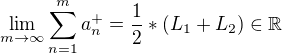 .
.
Druhý případ a případ, kdy řada konverguje neabsolutně, už určitě dáš dohromady:)
Offline
#3 05. 08. 2013 18:20
Re: Konvergence obecné řady
↑ Mihulik:
Mlátím se dlaní do čela. :-) Už je mi to jasné. Moc děkuju.
Offline
#6 05. 08. 2013 18:42
Re: Konvergence obecné řady
↑ Polopat:↑ Polopat:
To jsem rád - není zač:)
Řešení pomocí srovnávacího kritéria je samozřejmě snažší, ale když jsi to "neviděl", tak jsem to chtěl rozepsat co nejelementárněji:)
Offline
#7 05. 08. 2013 19:05 — Editoval vanok (05. 08. 2013 19:06)
Re: Konvergence obecné řady
Poznamka:
Co je uzitocne poznamenat a vediet je, ze 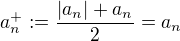 ak
ak 
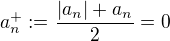 ak
ak 
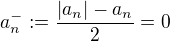 ak
ak 
 ak
ak 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergence obecné řady (TOTO TÉMA JE VYŘEŠENÉ)

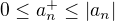 a
a