Matematické Fórum

klarinka.skaa · 12. 08. 2013 18:45

Byl by někdo ochotný poradit s tímto příkladem ?
Destička hmotnosti m=20 g je vertikálně zavěšena na pružině. Když na destičku položíme zaváží hmostnosti m1= 5g, protáhne se pružina o délku y1 do rovnovážné polohy systému (destička+ závaží). Po vychýlení z rovnovážné polohy kmitá tento systém s periodou T= 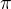$\pi$ / 3 s.
a) Určete, o jakou délku y1 se prodlouží pružina po vložení závaží na desku, je systém (destička+ závaží) v rovnováze. (5,5 cm)
b) určete silovou konstantu pružiny k (k=0,9 N/m)
c)Závaží o hmotnosti m1 zaměníme závažím o hmotnosti m2= 25 g. Určete posunutí 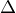$\Delta$ y mezi rovnovážnými polohami systémů (destička + závaží m1) a (destička+ závaží m2). ( 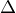$\Delta$ = 22 cm). DĚKUJU MOC

grizzlybear · 12. 08. 2013 23:14

a) co se týče velikosti prodloužení platí m1g=k.y1, kde neznáme k pružiny. To je podle vzorce
$\frac{2 \pi}{T}=\sqrt{\frac{k}{m}}$
Aby to vyšlo, je třeba vzít m= m(desky)+ m1 (závaží). Z toho pak vyjde 5,5 cm y1 (zhruba podle dosazení g).
b) Z toho co jsem popsal jde určit i k (překvapivě to vyjde jak má).
c) na céčko nemám sílu :)

klarinka.skaa · 14. 08. 2013 17:56

Děkuju moc

KennyMcCormick

c)

$m_2g=ky_2\Rightarrow y_2=\frac{m_2g}k$
$y_2=\frac{0,025\cdot9,81}{0,9}\dot=27,3\operatorname{cm}$

$\Delta y=21,8\operatorname{cm}$

Matematické Fórum

#1 12. 08. 2013 18:45

Kmity a vlnění

#2 12. 08. 2013 23:14

Re: Kmity a vlnění

#3 14. 08. 2013 17:56

Re: Kmity a vlnění

#4 17. 08. 2013 22:03 — Editoval KennyMcCormick (17. 08. 2013 22:04)

Re: Kmity a vlnění

Zápatí