Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 08. 2013 12:58
Integrál
Mohl by mi prosím někdo vysvětlit co to je a jak funguje integrál? Četl jsem definici na české wikipedii, ale nějak mi to nepomohlo, hlavně bych potřeboval příklad. Dal by se jako příklad integrálu použít výpočet poloh bodů x,y na kružnici opsané, vzhledem ke středu S?
Na té wikipedii na začátku jsou uveden= dva vzorce (nevím jak je sem opsat:
http://cs.wikipedia.org/wiki/Int egr%C3%A1l
je tam integrál a,b f(x) dx ... no a nechápu co znamená to dx. Prý ten vzorec vyjadřuje obsah plochy ve dvojrozměrné rovině, až na to že nechápu jak pomocí toho lze ten obsah vypočítat. Máte někdo nějaké příklady konkrétně k tomuto?
Pak tam je ta druhá část co jsem nepochopil:
"Pojmem integrál se občas označuje primitivní funkce F, jejíž derivací je funkce ƒ."
Co je to ta prim. funkce... a proč je v těch dvou F/f takový rozdíl?
Posledním bodem je základní věta analýzy:
"Nechť ƒ je spojitá reálná funkce na uzavřeném intervalu [a, b] a funkce F je primitivní k funkci ƒ. Potom hodnota (určitého) integrálu funkce ƒ na tomto intervalu je" vzorec ... Integrál a,b dx = F(b) - F(a)
co to teda znamená a konkrétní příklad, prosím.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#2 18. 08. 2013 14:07 — Editoval Aktivní (18. 08. 2013 14:40)
Re: Integrál
Integrování je proces opačný k derivování. Doporučuji nejdřív prostudovat to derivování než se začneš pouštět do tohoto :D
Máme funkci např. M(x), integrujeme ji neboli hledáme funkci, která je vůči funkci M(x) primitivní (nazveme si ji třeba D(x)). Pro funkci D(x) pak platí, že jestliže ji zderivujeme, získáme funkci M(x).
Řečeno ve vzorcích: INTEGROVÁNÍ: 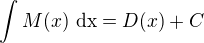 (v tomhle případě se přičte ještě konstanta, prostuduj ten pojem derivace)
(v tomhle případě se přičte ještě konstanta, prostuduj ten pojem derivace)
DERIVOVÁNÍ: 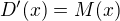
dx je jenom označení, říká nám že integrujeme podle proměnné x.
Na výpočet obsahů se používá určitý integrál, který je založený na odečtení horní hodnoty od dolní. Vezmu příklad:
Zkus spočítat obsah, který vyplní funkce f(x)=x v intervalu od 0 do 1. Stačí si to načrtnout nebo zobrazit, obsah se bude rovnat číslu 0.5.
A teď pomocí integrálu:
Víme že  (jeden ze základních vzorců)
(jeden ze základních vzorců)
Tohle použijeme pro určitý integrál: ![kopírovat do textarea $\int_{0}^{1}x\text{ dx}=[\frac{x^{2}}{2}]^{1}_{0}=\frac{1^{2}}{2}-\frac{0^{2}}{2}=\frac{1}{2}$](/mathtex/cb/cbdfbc0b32c7197e7cef5bc1904c8ef6.gif)
Prosím někoho znalejšího ať rovněž přispěje. Já sám jsem dost líný a tak jsem si ještě tyhle pojmy důkladně nenastudoval.. To víte, na škole to zatím neberem tak není kam spěchat :D
EDIT: Opraveno.
Offline
#3 18. 08. 2013 14:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
Zdravím oba :-)
(Prosím někoho znalejšího ať taky přispěje.)
Za to se také přimlouvám. Za sebe - řekla bych, že dobré začínat od historického úvodu a od fyzikálních aplikací a v textech přiměřených ZŠ, SŠ (např. sada Matematiky pro gymnázia má dobrý díl k tématu a dost srozumitelný.
Z online - materiály pana Reichla a studijní texty FO k matematice. Zdárné studium přeji.
↑ Aktivní:
jen drobnost - nevynechávej, prosím, v zápisu integrálů dx, sám povídáš že "dx je jenom označení, říká nám že integrujeme podle proměnné x" (tak alespoň proto).
Offline
#4 18. 08. 2013 14:49 — Editoval buff (18. 08. 2013 15:15)
Re: Integrál
Ale příklad jako takový mi je úplně k ničemu, protože to právě nechápu vysvětlování tímhle způsobem, spíš potřebuju něco obrazného. Nejsou někde nějaké stránky kde se to vysvětluje polopaticky a s obrázkama, ilustračními animacema?
K té potřebě naučit se integrální počty a derivace jsem se dostal přes tuto stránku. http://en.wikipedia.org/wiki/CIE_XYZ
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#5 18. 08. 2013 15:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
↑ buff:
v materiálech, co mám v odkazech, je to dobře vysvětleno + historické úvody jsou dost názorné, lepší, když si podle textu nakreslíš sám. Ale animace - např. zde na úvod právě zavedení geometrického použití integrálu pro výpočet obsahu, na závěr použití integrálů v geometrii.
Jinak si musíš sám zvážit, jak dobře se orientuješ ve funkcích - co už jsi prostudoval, jak jsi daleko ve studiu funkcí? Jinak je to trochu hop do hluboké vody - rovnou na integrál a zbytečně to může odradit.
Dal by se jako příklad integrálu použít výpočet poloh bodů x,y na kružnici opsané, vzhledem ke středu S?
ne, toto není dobrý příklad na integrály.
Offline
#6 18. 08. 2013 15:14
Re: Integrál
Mrknu na ten nový odkaz. To žluté pdf mi vyhovuje víc.
Jinak až ti to prostuduju, tak byste mi pak možná mohli pomoci ilustrovat na konkrétních grafech z této stránky (jež jsem prostudoval, ale schází mi pochopit tu matematickou část). Ty grafy vesměs představují 3 barvy viditelného světelného spektra (červená s nejdelší vlnovou délkou, zelená s prostřední vlnovou délkou a modrá s nejkratší vlnovou délkou), na ose x je zachycena vlnová délka a na y je zachycena zřejmě síla nebo intenzita barvy (předpokladám písmeno I). Zajímám se zejména o ty porovnávací funkce, které se potřebuju naučit (a pochopit). Graficky se to na grafu většinou znázorňuje trojúhelníkem (spojí se ty tři body - modrá, zelená, červená a vznikne trojúhelník). Mě by teda zajímalo jak to funguje, že ta funkce dokáže spočítat např. vzdálenost (asi diferenciál?) mezi červenou barvou a modrou barvou.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#7 18. 08. 2013 16:02 — Editoval buff (18. 08. 2013 16:06)
Re: Integrál
Tak koukám na to riemann-cz pdf na 3. stránku a už asi začínám chápat co znamenají ty čísla u toho 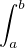 ,
, 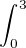 takhle jak to vidím přímo na tom grafu, tak je z toho jasné že se jedná o rozsah toho grafu na ose x.
takhle jak to vidím přímo na tom grafu, tak je z toho jasné že se jedná o rozsah toho grafu na ose x.
A kde na tom grafu je to x? tedy dx? Jsou to ty čísla 1,2,3 které nanášejí na osu x nebo to jsou ty reprezentany?
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#8 18. 08. 2013 16:03
- grizzlybear

- Příspěvky: 27
- Škola: MFF UK
- Pozice: student
- Reputace: 1
Re: Integrál
Na mě je to asi moc složitý... :)
http://en.wikipedia.org/wiki/CIE_XYZ
ale k odstavci Color matching functions.
Nejdříve integrál: udává plochu pod křivkou- (k ose x).
Druhak: plocha tam není znázorněna, protože tam není nikde 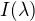 . Což je podle mě "barva", která nás zajímá. Tj. předmět, který vyzařuje v určitých vlnových délkách. Takže když známe I(lambda) můžem spočítat plochy pod křivkami (=spočíst integrály) a s čísly X,Y,Z dál pracovat. Celé se to (zas moje interpretace) děje proto, že člověk vnímá ve třech kanálech (
. Což je podle mě "barva", která nás zajímá. Tj. předmět, který vyzařuje v určitých vlnových délkách. Takže když známe I(lambda) můžem spočítat plochy pod křivkami (=spočíst integrály) a s čísly X,Y,Z dál pracovat. Celé se to (zas moje interpretace) děje proto, že člověk vnímá ve třech kanálech (
jak píšou na začátku)- tj. nevnímá celé spektrum, nebo alespoň celé viditelné spektrum (cca 400-700 nm). Navíc závisí na intenzitě. Tj. chápu to tak, že mám nějaké I(lambda) a ptám se, jak to asi bude lidské oko vidět?
Nevím, jestli jsem pomoh. :) Každopádně, není to lehké téma (jak ty integrály, tak vidění).
Offline
#9 18. 08. 2013 16:55
Re: Integrál
tie integraly predstavuju nejaky model ako sa konkretna bunka excituje pri danom svetelnom rozdeleni. napr. ta  zodpoveda asi cervenej, cervena sa vidi pomocou buniek na sietnici co obsahuju akesi farbivo (asi cervene). tu vie excitovat aj svetlo inej farby, trebars fialovej. a v oku mame tri typy buniek s tromi roznymi farbivami (farboslepym niekedy chyba jeden typ a maju iba dva mozno aj menej, tiez aj ine zivocichy mozu mat menej alebo viac) - kazda z nich sa excituje nejak inak pri danej farbe svetla - to predstavuje to rozlozenie intenzity
zodpoveda asi cervenej, cervena sa vidi pomocou buniek na sietnici co obsahuju akesi farbivo (asi cervene). tu vie excitovat aj svetlo inej farby, trebars fialovej. a v oku mame tri typy buniek s tromi roznymi farbivami (farboslepym niekedy chyba jeden typ a maju iba dva mozno aj menej, tiez aj ine zivocichy mozu mat menej alebo viac) - kazda z nich sa excituje nejak inak pri danej farbe svetla - to predstavuje to rozlozenie intenzity 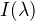 . a potom to ako sa nam naexcitovali jednotlive typy buniek (
. a potom to ako sa nam naexcitovali jednotlive typy buniek (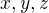 ) sa prenesie do mozgu a interpretuje ako dana farba. no a potom pocitace vyuzivaju to, ze sa dana farba da v mozgu vyvolat tak, ze namiesaju iba cervenu zelenu a modru (resp nejake ine tri) vo vhodnom pomere. nase oko a mozog nerozozna rozdiel medzi monochomatickym zelenym svetlom a nejakou vhodnou zmesou zltej a modrej.
) sa prenesie do mozgu a interpretuje ako dana farba. no a potom pocitace vyuzivaju to, ze sa dana farba da v mozgu vyvolat tak, ze namiesaju iba cervenu zelenu a modru (resp nejake ine tri) vo vhodnom pomere. nase oko a mozog nerozozna rozdiel medzi monochomatickym zelenym svetlom a nejakou vhodnou zmesou zltej a modrej.
ale teda poucenie
1) miesanie farieb nema nic spolocne s integralmi; samotne miesanie su len linearne kombinacie
2) integraly sa vyskytuju v modeli ktory nam hovori kolko ktorej farby by sme mali namiesat ak chceme dosiahnut efekt zodpovedajuci nejakemu dopredu danemu 
na to preco je takyto model zmysluplny treba nejaku fyziku a zisla by sa aj statistika, hlavne pojem strednej hodnoty
3) takyto rozklad do RGB (alebo xyz alebo ako si to chces nazvat) neobsahuje plnu informaciu o danom svetle, iny zivocich (napr. holuby su myslim tetrachromaty) by mohol rozlisit farby ktore sa nam javia ako rovnake
Offline
#10 18. 08. 2013 18:19 — Editoval buff (18. 08. 2013 18:46)
Re: Integrál
ještě jsem stále v tom žlutém pdf a napadlo mě, co se týče toho určitého integrálu na str. 13 tam se píše, že se "norma" postupně zvětšuje" dokud nedojdeme k uspokojivýmu výsledku (tedy aby se ti reprezentanti z daných intervalů vešly do té naší plochy grafu. Tak mě napadlo jestli ta norma (zde 0,05 je nějak vyjádřena tím vzorcem (Integrálem)? A taky jestli by šlo udělat integrál dy, takže by pak ty obdelníky byly vodorovné? Dále mě napadá, jestli existuje ještě jiná podobná metoda, ale která ma za cíl, aby se ty obdelníky nepřekrývali s křivkou grafu? Pouze se dotýkaly? Jen mě to tak napadlo. Asi by to mohlo být použitelné pouze u pravidelné křivky jako je sinusovka u střídavého napětí, apod. protože hodnoty na ose x by neměly pravidelný odstup...
Brano:
Tenhle typ grafu či "spektra" je odvozen od toho co je schopen vnímat člověk. Kdyby to spektrum bylo širší a uvnitř je nakreslený trojúhelník tak se tím dá vyjádřit více druhů rozsahu barev. Hádám, že tyhle šiřší gamuty jsou dobré pro převody barev, aby výpočty byly přesné a neztrácely se informace když např. nějakým způsobem upravíš digitální fotografii (jas, kontrast, odstín, saturace, atd.). Nevím jistě co myslíš pojmem střední hodnotou... Ale pokud vezmeš dvě barvy např. červenou a modrou a smícháš je tak máš fialovou.. myslíš toto? Anebo: pokud ubereš barvu z určité barvy, například z červené, sníží se její saturace či plnost a přibližuje se k šedé, tedy ke středu grafu, kde jsou šedé body, které neobsahují žádnou barvu. Asi je to ta limita červené barvy, protože 0 už není červená barva.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#11 18. 08. 2013 20:04 — Editoval Brano (18. 08. 2013 20:11)
Re: Integrál
nie pod strednou hodnotou som mal na mysli to, ze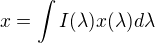 predstavuje strednu hodnotu premennej
predstavuje strednu hodnotu premennej  v rozdeleni danom hustotou
v rozdeleni danom hustotou  ; to je vec z teorie pravdepodobnosti a ked k tomu pridas nejaku fyziku tak prave ta predstavuje nejaku celkovu "excitaciu" (netusim ci to je spravny vyraz) bunky (resp. sady buniek s danym farbivom) ktorej schopnost absorbovat svetlo je popisana prave tou hustotou.
; to je vec z teorie pravdepodobnosti a ked k tomu pridas nejaku fyziku tak prave ta predstavuje nejaku celkovu "excitaciu" (netusim ci to je spravny vyraz) bunky (resp. sady buniek s danym farbivom) ktorej schopnost absorbovat svetlo je popisana prave tou hustotou.
pricom ta teoria nemusi nejak presne sediet s tym ako to v ludskom tele naozaj funguje, staci ak to ma spravny efekt, ked sa to pouzije v praxi. nakolko to sedi nemam zdania, lebo biologiu som nestudoval, podal som iba taku moju zjednodusenu predstavu a urcite su tu ludia co by to dokazali podat lepsie.
to co som tym chcel povedat je toto - kasli na integraly ak ta iba zaujima miesanie farieb - tie nakoniec aj tak miesas iba empiricky, t.j. hladas si na palete taku aka sa ti paci. a ak ta zaujma naozaj detailne ten model, tak iba integraly ti stacit nebudu, treba aj fyziku. pricom samozrejme vo fyzke sa bez derivacii, integralov a diferencialnych rovnic neda nikam pohnut.
PS: a ano samozrejme ten model je dostatocne vseobecny aby sa nejakymi modifikaciami dalo popisat vnimanie aj inych zivocichov, trebars bichromatov (2 farebne kanaly), alebo tetrachromatov (4 farebne kanaly) resp. upravit funkcie 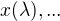 podla toho ake farbiva ich bunky obsahuju.
podla toho ake farbiva ich bunky obsahuju.
tym ze som sa na nich odvolaval som si chcel pomoct v tom aby som poukazal na to, ze je rozdiel v tom ake to svetlo je a ako ho vidime - ale tuto vetu treba brat tak trocha s rezervou
Offline
#12 18. 08. 2013 21:45
Re: Integrál
Brano, mě nejde o míchání barev ve smyslu malování, ale o porovnávání barev při programování postupů pro program.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#13 18. 08. 2013 22:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
buff napsal(a):
Brano, mě nejde o míchání barev ve smyslu malování, ale o porovnávání barev při programování postupů pro program.
Pokud mohu doporučit, jednodušší je napsat co máš v plánu programovat (případně podrobnosti okolo Tvého programování - případně přesuneme téma do AaP), možná se projasní, že tolik teorie okolo ani není třeba (nebo se projasní, co konkrétně je třeba).
buff napsal(a):
ještě jsem stále v tom žlutém pdf a napadlo mě, co se týče toho určitého integrálu na str. 13 tam se píše, že se "norma" postupně zvětšuje" dokud nedojdeme k uspokojivýmu výsledku (tedy aby se ti reprezentanti z daných intervalů vešly do té naší plochy grafu. Tak mě napadlo jestli ta norma (zde 0,05 je nějak vyjádřena tím vzorcem (Integrálem)? A taky jestli by šlo udělat integrál dy, takže by pak ty obdelníky byly vodorovné? Dále mě napadá, jestli existuje ještě jiná podobná metoda, ale která ma za cíl, aby se ty obdelníky nepřekrývali s křivkou grafu? Pouze se dotýkaly? Jen mě to tak napadlo. Asi by to mohlo být použitelné pouze u pravidelné křivky jako je sinusovka u střídavého napětí, apod. protože hodnoty na ose x by neměly pravidelný odstup...
a) "Norma dělení" jen udává jak rozdělíme úsečku (pod křivkou) na ose x, tedy jak velká bude strana každého malého obdélníku - při normě 0,05 máme úplně úzké proužky obdélníků o straně 0,05.
b) vodorovně být mohou, když nemáme funkci y=f(x), ale x=f(y) - někdy se to hodí použit.
c) je lepší, když obdélníky se překrývají s křivkou grafu, potom je menší chyba ve výpočtu - všimni si, že na jedné straně obdélníku jakoby nedostává do plného obsahu, naopak na druhé přebývá, tedy celkové se to skutečnému obsahu pod křivkou blíží lépe,
d) může to byt u různých (i "nepěkných na pohled") křivek, můžeme také obrazec rozdělit na díly podle "pěknosti" křivek, můžeme dokonce počítat i obsah obrazce, který není hezky uzavřen, ale jen se uzavření blíží (viz užití nevlastních integrálů).
Ale mám dojem, že zaměření na Tvůj program bude více účelné. Pro studium integrálů opět doporučuji materiály z příspěvku ↑ 3:.
Offline
#14 18. 08. 2013 23:06
Re: Integrál
jelena:
To zařazení mi vyhovuje. Pochopit integrály a derivace cítím jako nutnost a hlavně mi to dost dává. Dneska ten určitý integrál už chápu téměř kompletně až na nějaké detaily co se týče strany 15 kde nechápu jak došli k tomu vzorci xi-xi-1 nebo xi-1pak na str. 16 dole je věta 3. kde mě mate možnost použít interval [c,b] - měl jsem za to že v intervalu [a,b] musí být a nutně nalevo protože a<b, a tutíž bych očekával to samé u c, resp. [b,c] ne [c,b]. Na programování této funkce nepřekdu dokud se nenaučím základy k plnému pochopení teorie...
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#15 19. 08. 2013 10:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
↑ buff:
v pořádku, ovšem od kolegy Brano se dostane kvalitnějšího výkladu, než bude ten můj.
kde nechápu jak došli k tomu vzorci xi-xi-1 nebo xi-1
ten vzorec je "klíčový" v geometrickém použití integrálu pro výpočet obsahu (a pro zavedení pojmu integrál). Rozdělili úsečku na ose x na drobné úseky velikosti normy a počítají obsah malých obdélníků - na ose x vezmou vzdálenost mezi sousedními body dělení (proto 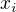 a
a 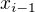 , nap5. mohu vzít mezi 5. bodem a 4. bodem, to bude
, nap5. mohu vzít mezi 5. bodem a 4. bodem, to bude 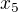 a
a 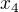 ). Tento rozdíl tvoří jednu stranu malého obdélníku. Potom vezmou bod "někde" na úsečce, to "někde" je ovšem takové, že mu přesně odpovídá hodnota funkce na křivce, tedy druhá strana obdélníku je
). Tento rozdíl tvoří jednu stranu malého obdélníku. Potom vezmou bod "někde" na úsečce, to "někde" je ovšem takové, že mu přesně odpovídá hodnota funkce na křivce, tedy druhá strana obdélníku je 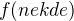 . Vynásobením délek stran dostanou obsah jednoho malého obdélníku:
. Vynásobením délek stran dostanou obsah jednoho malého obdélníku: pozor - zde a, b jsou délky stran obdélníku jak umíme vzorec pro obdélník, nejsou to a, b - hranice intervalu)
pozor - zde a, b jsou délky stran obdélníku jak umíme vzorec pro obdélník, nejsou to a, b - hranice intervalu)
A tak projdou obsahy všech malých obdélníku. Znak sumy  značí, že takové malé obsahy sečtou.
značí, že takové malé obsahy sečtou.
str. 16 dole je věta 3. kde mě mate možnost použít interval [c,b] - měl jsem za to že v intervalu [a,b] musí být a nutně nalevo protože a<b, a tutíž bych očekával to samé u c, resp. [b,c] ne [c,b].
c leží na intervalu od a do b, v pořadí  a rozděluji interval na menší dva podintervaly. Obsah každého počítáme určitým integrálem. Tedy počítáme nejdřív kousek od a do c (na intervalu [a,c]), potom kousek od c do b (na intervalu [c, b]). Když kousky slepíme, dostaneme celý obsah na intervalu [a, b].
a rozděluji interval na menší dva podintervaly. Obsah každého počítáme určitým integrálem. Tedy počítáme nejdřív kousek od a do c (na intervalu [a,c]), potom kousek od c do b (na intervalu [c, b]). Když kousky slepíme, dostaneme celý obsah na intervalu [a, b].
O tomto využití jsme již mluvili, že můžeme celou plochu rozdělit na plochy nad jednotlivými úseky podle "pěknosti" (využívá se, když plocha je tvořena z kousku různých funkcí například).
Offline
#16 19. 08. 2013 12:16
Re: Integrál
Jelena:
Skvělé vysvětlení, díky. Tam šlo o to že jsem nevěděl, že i znamená pořadí; ale je to to samé jako při programování používám ve smyčkách proměnnou n nebo i. Mimochodem si žena nebo muž? Je to sice ženské jméno, ale radši se zeptám.
I všem ostatním díky za vysvětlení.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#17 19. 08. 2013 13:16 — Editoval buff (19. 08. 2013 14:42)
Re: Integrál
Teď jsem si všiml že to X s dolním indexem i-1 je také v dolním indexu, to jsem ale neviděl. Kdyby to dali do závorky jako 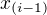 tak to dá hned smysl, ale koukám on ten index jde stejně špatně rozpoznat, velikost znaků x a -1mi přijde podobná takže to dost mate. Optický klam
tak to dá hned smysl, ale koukám on ten index jde stejně špatně rozpoznat, velikost znaků x a -1mi přijde podobná takže to dost mate. Optický klam
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#18 19. 08. 2013 13:33
Re: Integrál
to max {.., ..} to je definiční obor ? Max jako maximální přípustná hodnota a složené závorky se používají na definici pořadí? Jde o to že se musím naučit číst ty matematické zápisy, to mi nikdy moc nešlo. Chápu to tedy, že horní hodnota diferenciálu je menší o jedna než jeho předchozí hodnota a současně platí že hodnoty diferenciálu jsou větší než nebo rovno jedna. To poslední větší nebo rovno n, nevím jak přečíst
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#19 19. 08. 2013 13:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
↑ buff:
:-) žena, stačí pozorně sledovat slovesa v minulém času (mám např. "řekla").
Kdyby to daly do zavorky
:-) autorem odkazu je pan Robert Mařík, tak asi nebude daly.
to max {.., ..} to je definiční obor ?
máš na mysli povídání o "normě dělení" - ze vzdáleností mezi dělicími body bereme maximální hodnotu vzdálenosti - může se stát, že nejde podělit na stejné úsečky mezi krajními body - máme hodně stejných, ale (alespoň) jedna zůstane kratší (viz hned první obrázek, kde norma dělení 2, ale druhá úsečka je kratší).
Je to tak jasné?
Offline
#20 19. 08. 2013 14:40 — Editoval buff (19. 08. 2013 19:36)
Re: Integrál
Dotaz:
Tady v tom vzorci co znamená ta čárka nad písmeny x y z ?
http://upload.wikimedia.org/math/7/3/1/ … d6170a.png
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#21 19. 08. 2013 17:10 — Editoval Rumburak (20. 08. 2013 09:58)
Re: Integrál
↑ buff:
Ahoj. Uvedu ještě jeden pohled na integrál.
Mějme např. na intervalu  definovánu kladnou funkci
definovánu kladnou funkci  , jejímž grafem je křivka
, jejímž grafem je křivka  (o rovnici
(o rovnici 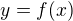 , jak jinak),
, jak jinak),
tedy  je na uvedeném intervalu spojitou funkcí.
je na uvedeném intervalu spojitou funkcí.
Zvolíme-li čísla 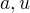 tak, aby
tak, aby  , je tím definován obrazec
, je tím definován obrazec  , jehož "základnou" je interval
, jehož "základnou" je interval 
na ose  , "pobočnými stranami" úsečky na přímkách o rovnicích
, "pobočnými stranami" úsečky na přímkách o rovnicích  a "střechou" ta část křivky
a "střechou" ta část křivky  , jejímž kolmým
, jejímž kolmým
průmětem na osu  je interval
je interval  .
.
Na číslo  pohlížejme jako na konstantu, zatímco na
pohlížejme jako na konstantu, zatímco na  jako na proměnnou. Obrazec
jako na proměnnou. Obrazec  , vlastně
, vlastně 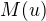 , nechť
, nechť
má obsah 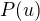 . Zkoumejme, jak funkce
. Zkoumejme, jak funkce  souvisí s funkcí
souvisí s funkcí  . K tomu pevně zvolme
. K tomu pevně zvolme  . Z předpokladů o funkci
. Z předpokladů o funkci 
plyne, že je spojitá v bodě  , tedy - podle definice spojitosti - k libovolně malému
, tedy - podle definice spojitosti - k libovolně malému  existuje
existuje  takové, že
takové, že
(1) pro každé 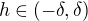 je
je  .
.
Zvolme  , k němu vezměme
, k němu vezměme  z předchozího výroku a uvažujme
z předchozího výroku a uvažujme 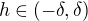 . Přidejme nejprve předpoklad
. Přidejme nejprve předpoklad  .
.
Obrazec 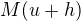 vznikne z
vznikne z 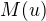 prodloužením jeho základny z
prodloužením jeho základny z  na
na 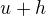 , tedy připojením svislého "proužku" o šířce
, tedy připojením svislého "proužku" o šířce  ,
,
jehož obsah 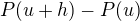 vyhovuje nerovnosti
vyhovuje nerovnosti
(2)  ,
,
jak plyne z (1) (k lepšímu pochopení pomůže obrázek) . Úpravou (2) obdržíme
 ,
,
 ,
,
pro 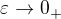 a z definice jednostranné derivace odtud dostáváme
a z definice jednostranné derivace odtud dostáváme 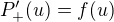 .
.
Pro  bychom obdobnou úvahou obdrželi
bychom obdobnou úvahou obdrželi 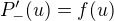 , což spolu s předchozím výsledkem dávé
, což spolu s předchozím výsledkem dávé 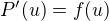 .
.
Tedy na uvažovaném intervalu je  primitvní funkcí k
primitvní funkcí k  , a sice taková, že
, a sice taková, že 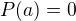 , jak je zřejmé. Taková funkce
, jak je zřejmé. Taková funkce  existuje
existuje
právě jedna. Jestliže (na uvažovaném intervalu) je  obecně jiná p.f. k
obecně jiná p.f. k  než
než  , potom zde identicky platí
, potom zde identicky platí 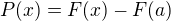 ,
,
speciálně pro  bude
bude 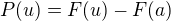 .
.
Obsah našeho obrazce 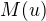 je tedy roven hodnotě
je tedy roven hodnotě 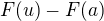 , kde
, kde  je libovolná primitivní funkce k
je libovolná primitivní funkce k  na intervalu
na intervalu  .
.
Za uvedené situace pak číslo 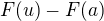 nazýváme Newtonovým "integrálem funkce
nazýváme Newtonovým "integrálem funkce  od
od  do
do  " a píšeme
" a píšeme
 .
.
Vzhledem k velké rozmanitosti funkcí byly hledány i další definice integrálu (tj. metody, jak počítat především obsah obrazce, jehož hranice je složena
případně i ze složitějších křivek, než jsou úsečky). Jednou z nich je i definice Riemannova založená na tom, že omezená funkce integrovaná na uzavřeném
intervalu je aproximována zdola i shora pomocnými funkcemi, které jsou po částech konstantní.
Neexistuje "obecná" integrační metoda použitelná na všechny případy funkcí. Každá z takových metod funguje pouze na určité třídě funkcí a má své
výhody i nevýhody . Jdou-li na určitou funkci použít dvě integrační metody, vedou ke stejnému výsledku. Na obzvláště jednoduché případy, jakými jsou
funkce spojité na uzavřeném intervalu, fungují všechny integrační metody (s týmž výsledkem).
Offline
#22 19. 08. 2013 17:22
Re: Integrál
↑ Rumburak:
jak jsem již psal, mě je spíše srozumitelné když vidím obrázky a grafy tak jako je to tady:
http://is.muni.cz/elportal/estud/prif/p … ann-cz.pdf
ale ty asi mluvíš o neurčitém integrálu a tomu bych se rád věnoval možná tak zítra nebo pozítří jestli najdu nějakou podobně ilustrativní příručku jako je ta nahoře. Vzorce samotné tak jak je píšeš nechápu.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#23 19. 08. 2013 20:10 — Editoval buff (19. 08. 2013 20:11)
Re: Integrál
Může mi někdo vysvětli ten vzorec na str. 28 dole ?
http://is.muni.cz/elportal/estud/prif/p … ann-cz.pdf
Je tam součet hodnot yi = S
h je asi diferenciál
hS/2 = S/20 = nějaké číslo které je výsledkem integrálu [1,2] kde je funkce f ((sin x) / x) dx.n
Což nechápu co je to číslo zač.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#24 19. 08. 2013 22:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
buff napsal(a):
Dotaz:
Tady v tom vzorci co znamená ta čárka nad písmeny x y z ?
http://upload.wikimedia.org/math/7/3/1/ … d6170a.png
To jsou trichromatické členitele - podrobně na str. 2 v odkazu.
Je tam součet hodnot yi = S
h je asi diferenciál
hS/2 = S/20 = nějaké číslo které je výsledkem integrálu [1,2] kde je funkce f ((sin x) / x) dx.n
Což nechápu co je to číslo zač.
h je délka malé úsečky, ze kterých se skládá celý interval, na kterém integrujeme (podělili jsme na n=10 dílů a dostali jsme h=0.1 délku každého dílu). Je to přibližná metoda výpočtu integrálu - abych pravdu řekla, tak nevím, jak metodu použiješ pro své programování.
Pro mne je trochu obtížné si najít motivaci pro toto téma a kolegu ↑ Rumburak: obdivuji za ochotu (a o to větší zklamání mám, když takový příspěvek nenajde odezvu). Velmi velké zklamání.
Kolegu Rumburaka zdravím.
Offline
#25 20. 08. 2013 08:24 — Editoval buff (20. 08. 2013 08:38)
Re: Integrál
↑ jelena:
Díky, našel jsem ještě jeden odkaz kde to je dobře popsáno:
"Dopadá-li světlo určitého spektrálního složení do oka, vzniká v mozku barevný vjem, barva. Světlo je charakterizováno světelným tokem, který je mírou účinnosti světla při vyvolání vjemu jasu, vlnovou délkou jíž odpovídá vjem barvy zvaný tón a čistotou jíž odpovídá sytost. Subjektivní barevné vjemy můžeme vyjádřit číselnými hodnotami, které přesně vystihují barvu. Podle normy Mezinárodní osvětlovací komise (CIE) z roku 1931, vzniklé na základě měření velkého počtu pozorovatelů, se předpokládá, že oko vnímá třemi
orgány, jejichž citlivost k barvám je vyjádřena barevnými podněty (trichromatickými členiteli) x(λ) , y(λ) , z(λ) spektrální barvy vlnové délky λ . Barevnými souřadnicemi (trichromatickými souřadnicemi) příslušné
spektrální barvy nazýváme veličiny"
a následuje vzorec který neumím opsat a vlastně neumím přečíst to x s čárou nahoře. To se ve vzorci asi nečte jako x s čarou.
x + y + z = 1
Protože platí x + y + z = 1, stačí k definici barvy znát jenom dvě z těchto
veličin. Barevné podněty, v závislosti na vlnové délce světla, jsou znázorněny
na obr.8."
x=(x s čarou nahoře) / (x s čarou nahoře) + (y s čarou nahoře) + (z s čarou nahoře)
No já bych to nazýval asi vstupem raději než tím složitým slovem co si nezapamatuju. Článek popisuje měření propustnosti, takže je jasné, že jsou nějaké hodnoty na vstupu (podněty) a nějaké na výstupu (výsledek), podobně jak u té funkce y=f(x). Vstupy jsou na ose x a výstupy na ose y.
PS: Vždyď ono to není těžké si to zapamatovat tri+chroma ... Ale ten název platí pouze v optice a já věřím, že ta čárka nad x se používá obecně i v jiných oborech...
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline