Matematické Fórum

vviston · 22. 08. 2013 12:02

Ahoj, rád bych se zeptal, jak z hlavy pohodlně dávat mocniny typu

(1/8) ^ x = 4

Vím, že x má být záporné, abych se poté dostal na zlomek typu 1/ něco a to něco by mělo být 1/4 aby poté platila rovnost 1/(1/4) = 4 což je pravda, ale moc nevím, jakým postupem zjistit ten exponent na který mocnit ? Vím, že je to hloupý dotaz a jistě mi to pak dojde, ale nějak na to nemám nervy. Díky

BakyX · 22. 08. 2013 12:23

$\frac{1}{8}=\frac{1}{2^3}=2^{-3}$

$4=2^2$

Takže $-3x=2$

Eratosthenes · 22. 08. 2013 12:28

↑ vviston:

Ahoj,

to není zrovna moc hezký příklad. Kdyby to bylo (1/16) ^ x = 4, pak si stačí uvědomit, že 16^(1/2)=4, a protože je ta šestnáctka dole, je x= -1/2. U příkladu, který uvádíš, je nejlépe si pomoct logaritmy:

$\left(\frac 1 8\right) ^x = 4 \Rightarrow x\cdot \log \frac 1 8 = \log 4.$

Principiálně je jedno, jaký dáš základ, prakticky je dobré volit podle zadání - tedy v tomto případě buď osmičku nebo čtverku (a nejlépe dvojku). Tento postup funguje samozřejmě i na "průhledné" příklady typu (1/16) ^ x = 4.

Freedy · 22. 08. 2013 13:17 — Editoval Freedy (22. 08. 2013 13:17)

↑ Eratosthenes:
Proč používat logaritmy tam, kde snadno najdeš celočíselý základ? zbytečnost

Brano · 22. 08. 2013 13:22

↑ Freedy:
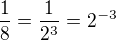
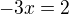
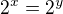Ak z rovnosti $2^x=2^y$ dedukujes $x=y$ tak si vpodstate pouzil logaritmus s celociselnym zakladom.

Matematické Fórum

#1 22. 08. 2013 12:02

Mocnění záporným exponentem

#2 22. 08. 2013 12:23

Re: Mocnění záporným exponentem

#3 22. 08. 2013 12:28

Re: Mocnění záporným exponentem

#4 22. 08. 2013 13:17 — Editoval Freedy (22. 08. 2013 13:17)

Re: Mocnění záporným exponentem

#5 22. 08. 2013 13:22

Re: Mocnění záporným exponentem

Zápatí