Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 22. 08. 2013 11:30
Re: Limita
Co říkáte na můj popis "vzdálenosti proměnné k limitě"?
"Vzdálenost proměnné na ose y - vyjádřená epsilonem (e) nebo na ose x - vyjádřená deltou (d), je maximální vzdálenost, na kterou se může proměnná přiblížit k funkční hodnotě y=f(x). Za tuto vzdálenost se nemůže přiblížit (narůst nebo klesnout - v závislosti na směru funkce)." Tam bych dodal, že vzdálenost může být 0.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#27 22. 08. 2013 11:47
Re: Limita
Takže teď to o té vzdálenosti shrnu ještě jednou:
Vzdálenost proměnné k limitě, e - d
Vzdálenost proměnné na ose y - vyjádřená epsilonem (e) nebo na ose x - vyjádřená deltou (d), je maximální vzdálenost, na kterou se může proměnná přiblížit k funkční hodnotě y=f(x). 
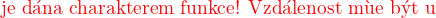

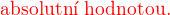
Za tuto vzdálenost se nemůže přiblížit (narůst nebo klesnout - v závislosti na směru funkce). Proto obrazně nazývám tuto vzdálenost paddingem.
Vzdálenost nemusí být vždy lineární, např. při a=0, f(x)=x^2 je d=odmocnina z e
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#29 22. 08. 2013 12:16
Re: Limita
↑ buff:
Pokud definici výroku  , kde
, kde  jsou reálná čísla, vezmeme ve tvaru
jsou reálná čísla, vezmeme ve tvaru
(1) "ke každému  existuje
existuje  takové, že pro každé
takové, že pro každé  splňující
splňující  je
je  " ,
" ,
což je jedna z možných navzájem ekvivalentních variant, a vezmeme-li některou dvojici čísel 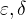 z tohoto výroku, potom přesně lze říci toto:
z tohoto výroku, potom přesně lze říci toto:
(2) Je-li vdálenost bodů  (na ose x) nejvýše
(na ose x) nejvýše  , potom vzdálenost bodů
, potom vzdálenost bodů  (na ose y) je nejvýše
(na ose y) je nejvýše  .
.
Ale když  ponecháme a ono k němu nalezené
ponecháme a ono k němu nalezené  zmenšíme (jen tak, aby zůstalo > 0) , potom výrok
zmenšíme (jen tak, aby zůstalo > 0) , potom výrok
"pro každé  splňující
splňující  je
je  " ,
" ,
který je částí výroku (1) , bude stále platit. Takže nikde není zaručeno, že to "první"  bylo ke zvolenému
bylo ke zvolenému  maximální možné
maximální možné
a pro definici limity by to ani nebylo důležité.
Offline
#30 22. 08. 2013 12:17 — Editoval buff (22. 08. 2013 12:20)
Re: Limita
e - d
Pozn. to nebyl vzorec ale pomlčka mezi epsylonem a deltou... aby vás to nezmátlo
A to co jsem chtěl napsat červeně, ale koukám že se to tam nevešlo:
"Maximální vzdálenost, na kterou se může přiblížit, je dána charakterem funkce! Vzdálenost může být u jedné funkce 0 a u jiné bude nějaké kladné číslo vyjádřené absolutní hodnotou. "
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#31 22. 08. 2013 12:30
Re: Limita
jarrro napsal(a):
↑ buff:tomu nerozumiem. predsa ak existuje limita tak sa k nej môžeš (musíš, inak by neexistovala) ľubovoľne priblížiť
A ke které větě se vyjadřuješ?
Rumburakem doplněná/opravená moje "definice" je:
"Limita L funkce f(x) v bodě a znamená, že když se proměnná x nekonečně blíží k bodu a, potom hodnota f(x) se nekonečně blíží k L ."
Čili pro tuto situaci se může f(x) přiblížit jen po danou hranici/blízkost/vzdálenost... za tuto vzdálenost jít nemůže.
Ale moje definice ze včerejška byla určitě špatně - to bylo "Limitu tedy chápu jako dolní hranici toho intervalu, ke které se x nebo y může nekonečně přibližovat."
Jenže ta vzdálenost není limita... ale vzdálenost k limitě.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#32 22. 08. 2013 12:35
Re: Limita
↑ buff:reagoval som na
buff napsal(a):
Vzdálenost proměnné na ose y - vyjádřená epsilonem (e) nebo na ose x - vyjádřená deltou (d), je maximální vzdálenost, na kterou se může proměnná přiblížit k funkční hodnotě y=f(x)
MATH IS THE BEST!!!
Offline
#33 22. 08. 2013 12:53 — Editoval buff (22. 08. 2013 12:53)
Re: Limita
↑ jarrro:
No tak z grafu a z toho co tu padlo jsem to pochopil tak, že mezi tou limitou může být nějaká vzdálenost: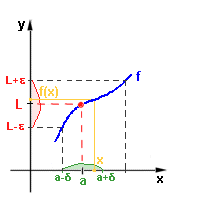
Jenže teď když se na to znova dívám tak mě to opět mate. Proč kreslili do grafu epsilon a delta, když ta křivka je spojitá? Takže bych tam právě tu hranici (černá přerušovaná čára) neočekával. Očekával bych takovou hranici tam kde křivka je přerušená a pak bych x neočekával uvnitř těchto přerušovaných čar, ale mimo ně.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#35 22. 08. 2013 13:30 — Editoval jarrro (22. 08. 2013 13:35)
Re: Limita
↑ buff:obrázok je dobre. je jedno či je spojitá či nie funkčná hodnota v bode a je nepodstatná
musíš si uvedomiť, že limita je o tom, že k ľubovoľne danému epsilon musí delta existovať stačí sa pozrieť na ten obrázok a vidíš, že aj keby bol ten červený krúžok prázdny a funkčná hodnota by neexistovala prípadne bola inde tak to na situácii nič nemení
iná situácia je 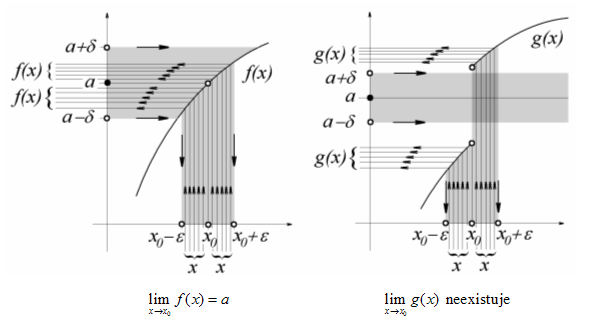
je ten druhý obrázok aj keď je tam prehodené epsilon s deltou neviem prečo, ale to je v princípe jedno ako nazveš len treba dodržať poradie, že k okoliu limity hľadáš okolie bodu, ale pre malé (v tomto prípade) delta nenájde vhodné epsilon a nenájde ani keď zmení predpokladanú hodnotu a. pokiaľ sa s a presunie do vrchného bodu tak platí len podobne v dolnom bode
podobne v dolnom bode
v prvom prípade ide o limitu sprava a v druhom zľava pričom tie limity sú rôzne teda obojstranná limita neexistuje
MATH IS THE BEST!!!
Offline
#36 22. 08. 2013 18:56 — Editoval buff (22. 08. 2013 18:57)
Re: Limita
Mám tomu rozumět tak, že funkce má limitu, i když jejím výsledkem není žádná hodnota? Jako že je to jen bod v grafu pro danou funkci, který tam bude i kdyby tam nebyla křivka funkce?
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#38 22. 08. 2013 20:02
Re: Limita
Asi to nikdy nepochopím :-(
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#39 22. 08. 2013 22:14
Re: Limita
Díval jsem se na dvě videa od tohohle borce:
a z toho se mi to zdá jasný.
http://www.youtube.com/watch?v=0kDWVxFbU4A
http://www.youtube.com/watch?v=SCox1RkkgAo
Zde dobře podané a ta ilustrace přímo na tabuli mi přijde lepší.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#40 22. 08. 2013 22:59 — Editoval buff (22. 08. 2013 23:00)
Re: Limita
Čili jde jen o to dosadit x, abych si vypočítal tu limitu a zjistil jestli je to jednostranná nebo oboustranná limita. Pokud je ta funkce spojitá, tak limita je rovna funkční hodnotě. Pokud to není funkce spojitá, tak mi vyšly dvě limity (různé čísla) a tak říkáme, že celkově limita neexistuje. Na tom druhém videu je to takto popsáno v čase 8:38.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#42 23. 08. 2013 08:15
Re: Limita
Takže dík za snahu. Myslím že s pomocí těch videí už to nějak zvládnu. Možná že člověk snadněji pochopí to co je na tabuli, přeci jen ten mozek je někdy možná zvyklý právě na to že nám to ti učitelé min. 8 let vysvětlovali slovem a ilustracemi na tabuli.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#43 23. 08. 2013 08:20
Re: Limita
↑ buff:
Pojem limity funkce patří k základním pojmům diferenciálního počtu. Mít limitu je lokální vlastnost funkce popisující chování funkce v ryzím okolí bodu, v němž limitu určujeme. Skutečnost, že jde o ryzí okolí (tj. okolí kromě tohoto bodu), znamená, že limita nezávisí na funkční hodnotě funkce v tomto bodě — funkční hodnota se může lišit od limity v tomto bodě, nebo funkce nemusí být v daném bodě definovaná. Spojitost funkce má lokální nebo globální charakter. Spojitost funkce v daném bodě znamená, že limita funkce v daném bodě je rovna funkční hodnotě v tomto bodě.
Offline
#44 23. 08. 2013 11:17 — Editoval Rumburak (23. 08. 2013 16:03)
Re: Limita
Asi to nikdy nepochopím :-(
K tomu jen pár poznámek.
Matematické definice mohou být "statické" , jako např.  , nebo "dynamické" opírající se o nějaký výrok,
, nebo "dynamické" opírající se o nějaký výrok,
který (zpravidla jinými slovy) v podstatě říká, co se stane, když ... .
Tyto "dynamické" definice (vkládám do uvozovek, protože nejde o termín, ale pouze o můj momentální nápad) jsou obtížně
srozumitelné dokonce i mnohým vysokoškolákům na oborech ekonomichých ba i technických, pokud se s nimi setkávají
poprvé. K jejich pochopení je důležité podrobně je rozebrat "slovo od slova" a nic nepřehlédnout. Matematika se liší
např. od poesie tím, že každý (správně formulovaný) matemtický výrok je míněn NAPROSTO DOSLOVA, bez metafor, bez
jinotajů (prostoru něco si domýšlet) a pod. Lidé, kteří nejsou zvyklí se takto exaktně sami vyjadřovat, mívají s matematikou
problémy, protože pak ani nedovedou správně číst matematické formulace.
Přečetl jsem si teď znovu některé Tvé slovně formulované myšlenky, např.
Čili jde jen o to dosadit x, abych si vypočítal tu limitu a zjistil jestli je to jednostranná nebo oboustranná limita.
Dosadit CO , KAM a ZA CO ?
mezi tou limitou může být nějaká vzdálenost
Mezi tou limitou A ČÍM ?
"Vzdálenost proměnné na ose y - vyjádřená epsilonem (e) nebo na ose x - vyjádřená deltou (d), je maximální vzdálenost, na kterou se může proměnná přiblížit k funkční hodnotě y=f(x). Za tuto vzdálenost se nemůže přiblížit (narůst nebo klesnout - v závislosti na směru funkce)." Tam bych dodal, že vzdálenost může být 0.
Představ si, že by to někdo řekl Tobě. Rozměl bys tomu ?
Zkrátka: jinotaj vedle jinotaje, protože - odhaduji - nechceš si dát práci zformulovat ty myšlenky PŘESNĚ (není to moralisující výtka,
jen pokus podat Ti jakési zrcadlo pro případ, že bys měl zájem do něho pohlédnout ). Podobně si patrně nechceč dát tu praáci analysovat
složitější matematickou definici, což Ti ale zároveň přidělává práci jinou - a troufám si říci, že mnohem objemnější - vynaloženou při
zdlouhavých diskusích na tomto foru. Nemyslím si, že bys byl proto obecně "lenoch" nebo "lempl", prostě ve slovním vyjadřování nejsi
na věcnou přesnost zvyklý, básnická vzletnost je Ti patrně bližší :-) .
Offline
#45 23. 08. 2013 13:13
Re: Limita
Ani nevím jak se přesněji vyjádřit, ne že si nechci dát práci.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#46 23. 08. 2013 16:00 — Editoval Rumburak (23. 08. 2013 16:17)
Re: Limita
↑ buff:
Je to částečně otázka osobního založení, částečně otázka praxe. Myslím, že z matematické látky ZŠ mají v uvedeném směru
nejsilnější didaktický efekt geometrické konstruktivní úlohy, jsou-li pečlivě řešeny do všech detailů (rozbor, konstrukce,
důkaz, diskuse) , a pak slovní úlohy řešené pomocí rovnic.
Ukázal jsem Ti zatím tři příklady, kde by formulace šly vylepšit, a u těch dvou nejjednodušších jsem i napověděl kterým směrem.
Je možné, že už toto Tě posune o kus dál.
EDIT.
Vlastně je to podobné, jako když píšeš program. Počítači také musíš sdělit ZCELA PŘESNĚ, co a jak má v daný moment udělat,
jak má reagovat na události, jak má naložit se vstupními daty atd.
Offline
#47 23. 08. 2013 16:09
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Limita
↑ jarrro:
===============
je tam prehodené epsilon s deltou neviem prečo
===============
Vůbec jsem si toho nevšiml :-))))
V principu je to sice jedno, ale ustáleno je to opravdu naopak.
Budoucnost patří aluminiu.
Offline
#48 24. 08. 2013 08:17
Re: Limita
Nevíte někdo co to v angličtině znamená "RMSE difference"? Je to něco s derivací nebo diferenciálem?
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#50 24. 08. 2013 10:44
Re: Limita
jarrro napsal(a):
↑ buff:podľa mňa ani s jedným aspoň google vyhadzuje root mean square error čo je odmocnina strednej kvadratickej chyby
Nevím co to je, ale jde o tento vzorec
sqrt((reddiff^2+greendiff^2+bluediff^2)/3)
red, green, blue jsou barvy v CIE RGB prostoru
http://www.normankoren.com/CIE_xy_Adobe_sRGB.jpg
reddiff, greendiff a bluediff nevím co znamená. Těch vzorečků co bych chtěl vysvětlit je víc, takže mohu založit nové téma, aby se to nepletlo dohromady s limitou. Podle toho jestli to s limitou má něco do činění nebo ne.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
