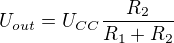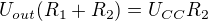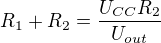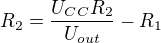Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 29. 08. 2013 16:20
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Vyjádření neznámé ze vzorce
↑ Freedy:
To bych nenazval vyjadrenim, protoze R2 je porad na obou stranach.
↑ Davilius:
Offline
#4 29. 08. 2013 17:45 — Editoval Freedy (29. 08. 2013 17:45)
Re: Vyjádření neznámé ze vzorce
xDD nevšim sem si toho :D pardon :DD
samozřejmě uprava kolegy správná, kdybych to nepřehlédl, byla by stejná
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline