Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
.#2 31. 08. 2013 14:01
Re: Vyjádření roviny v A4
Ahoj,
jedná se o nadrovinu v prostoru dimenze 4. Je to trojrozměrný prostor, který je podmnožinou A4. Analogická představa rovina-přímka; 3D prostor-rovina; 4D prostor-např.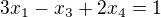 
.
Parametrické vyjádření se hledá úplně stejně jako v případě trojrozměrného prostoru a přímky zadané v takovémto tvaru. Jediná nevýhoda je, že se to špatně představuje.
Offline
#3 31. 08. 2013 14:15 — Editoval Rumburak (31. 08. 2013 14:18)
Re: Vyjádření roviny v A4
Ähoj .
V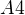 
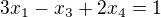je rovnicí NAROVINY, což je obecně lineál, jehož dimese je o 1 menší než dimense celého prostoru.
V našem případě je dimense prostoru 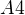rovna 4, takže 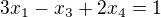je rovnice lineélu dimense 3.
Dvoudimesionální rovina v 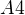pak je jakousi průsečnicí dvou vhodných lineálů dimense 3 (analogicky jako když přímka v 
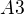je
průsečnicí dvou různoběžných rovin).
Koeficiety v rovnici 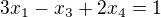určují normálový (k nadrovině kolmý) vektor m = (3, 0, -1, 2) , druhá nadrovina má
normélový vektor n = (1, -4, 2, 0) . Hledaná rovina, která je jejich průsečnici, bude kolmá o oběma vektorům m, n, tutéž vlastnost
musí mít i její směrové vektory a, b, které hledáme. Budou navíc lin. nezávislé, tedy bází ortogonáího doplňku k lieneárnímu obalu
vektorů m, n.
Offline