Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 09. 2013 14:22
vypocet smerodatne odchylky dle wikipedie
Dobrý den,
na wikipedii jsem hledal vztah pro vypocet smerodatne odchylky. ( viz http://cs.wikipedia.org/wiki/Sm%C4%9Bro … 1_odchylka)
,zustal jsem ovsem nad jednim vzorcem stát. Zde se totiž píše že průměr ( na druhou ) pod odmocninou lze pocitat soucasne s vypoctem ctvercu x(i). Může to vůbec správně vyjít? Vždyť takový průměr nebude vypovídat nic o celém souboru dat. (resp. až u poslední hodnoty ano)
Co si o tom myslíte, nenapsal to nějaký diletant?
nikee
Offline
#2 02. 09. 2013 15:02
Re: vypocet smerodatne odchylky dle wikipedie
Na tom vzorci nevidim nic podezreleho a v jakem smyslu ma byt toto zajimava uloha?
„Jestliže neumíš – naučíme, jestliže nemůžeš – pomůžeme ti, jestliže nechceš – nepotřebujeme tě.“ —Jan Werich
Offline
#3 02. 09. 2013 15:12
Re: vypocet smerodatne odchylky dle wikipedie
↑ Geronimo:
Zdravim,
ja jsem to napsal, protoze se mi nezda, ze by se v jedne iteraci dal pocitat prumer a soucasne v te same iteraci ho jiz aplikovat. Vůbec mi to nesedí.
Offline
#4 02. 09. 2013 15:54
Re: vypocet smerodatne odchylky dle wikipedie
Bavime se o tomto vzorci?
Vzdyt to preci neni vubec iterace. Na zacatku mas  pozorovani, na jejichz zaklade si vypocitas zvlast prumer, a potom dosadis do vyse uvedeneho vzorce a vypocitas smerodatnou odchylku.
pozorovani, na jejichz zaklade si vypocitas zvlast prumer, a potom dosadis do vyse uvedeneho vzorce a vypocitas smerodatnou odchylku.
„Jestliže neumíš – naučíme, jestliže nemůžeš – pomůžeme ti, jestliže nechceš – nepotřebujeme tě.“ —Jan Werich
Offline
#5 02. 09. 2013 16:08
Re: vypocet smerodatne odchylky dle wikipedie
↑ Geronimo:
Omlouvám se, ale současně děkuji za diskuzi. Měl jsem na mysli třetí vzorec u tématu "Výběrová směrodatná odchylka, kde se píše cit:
Pro praktické výpočty se častěji používá ekvivalentní vzorec, který nevyžaduje předběžný výpočet průměru. Druhý sčítanec pod odmocninou totiž lze počítat průběžně zároveň s výpočtem sumy čtverců xi během jediného programového cyklu procházejícího vstupní data. Pokud je N velké, redukuje se tím doba výpočtu zhruba na polovinu. Za určitých okolností však tato metoda zároveň může zvýšit vliv zaokrouhlovacích chyb na přesnost výsledku.
S pozdravem
Offline
#6 02. 09. 2013 16:23
Re: vypocet smerodatne odchylky dle wikipedie
Aha, v tomto pripade taky nejde o iteraci, ze by se v kazdem kroku pocital znovu prumer. Ten upraveny vzorec dovoluje pocitat prumer nezavisle na kvadratu 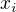 a tedy muzeme pouzit jeden cyklus. Kdyby se pocital prumer zvlast, tak musime pouzit dva cykly - prvni na vypocet prumeru, druhy na vypocet smerodatne odchylky. Timto zpusobem lze usetrit vypocetni kapacity.
a tedy muzeme pouzit jeden cyklus. Kdyby se pocital prumer zvlast, tak musime pouzit dva cykly - prvni na vypocet prumeru, druhy na vypocet smerodatne odchylky. Timto zpusobem lze usetrit vypocetni kapacity.
„Jestliže neumíš – naučíme, jestliže nemůžeš – pomůžeme ti, jestliže nechceš – nepotřebujeme tě.“ —Jan Werich
Offline
#7 04. 09. 2013 20:22
Re: vypocet smerodatne odchylky dle wikipedie
↑ Geronimo:
Takže než vypočteš celý vztah, potřebuješ stejně jeden cyklus pro výpočet průměru a druhý pro výpočet směrodatné odchylky, takže to vyznělo zavádějicně na wikipedii.
Zdravím
Offline
#8 04. 09. 2013 20:38
Re: vypocet smerodatne odchylky dle wikipedie
↑ nikee.x: ne. čemu jsi nerozuměl na "jeden cyklus"?
Offline
#9 04. 09. 2013 20:47
Re: vypocet smerodatne odchylky dle wikipedie
↑ nikee.x:
A že jsem tak zvědav, v jakém jazyce programuješ? Jazyk, který neumožňuje manipulaci s více než jednou proměnnou v jednom cyklu, je až roztomile zvrácený.
Доктор сказал «в морг» — значит в морг!
Offline
#10 07. 09. 2013 13:53 — Editoval nikee.x (07. 09. 2013 14:20)
Re: vypocet smerodatne odchylky dle wikipedie
↑ Stýv:
Ono to u mě není v tom, že bych nedokázal přepsat vzorec z wikipedie do nějakého "vyššího" programovacího jazyka, dělal jsem např. C++ nebo C#.
Můj problém je v tom, že ten vzorec, kde by se průměr počítal průběžně, na mě dělá dojem, že ten průměr bude v danou chvíli spočítán jen z (i) prvků. Prostě to nechápu. Myslím toto tvrzení:
Druhý sčítanec pod odmocninou totiž lze počítat průběžně zároveň s výpočtem sumy čtverců xi během jediného programového cyklu procházejícího vstupní data.
Offline
#12 16. 09. 2013 18:42
Re: vypocet smerodatne odchylky dle wikipedie
Průměr_z_N_plus_jedna_hodnot = (Průměr_z_N_hodnot * Počet_N_hodnot + Nová_hodnota) / (Počet_N_hodnot + 1)
A můžeš pokračovat.
Počet_N_hodnot se pak samozřejmě zvýší o 1.
Offline
#13 16. 09. 2013 18:56 — Editoval Brano (16. 09. 2013 19:08)
Re: vypocet smerodatne odchylky dle wikipedie
pisu o tomto: vstup x_i pre i=1..n a vystup ma byt A - priemer a B - odchylka (vychylena - t.j. ta s n-kom v menovateli)
metoda 1 - podla vzorca 1
A=B=0
for i in 1..n A=A+x_i
A=A/n
for i in 1..n B=B+(x_i-A)^2
B=B/n
metoda 2 - podla vzorca 2
A=B=0
for i in 1..n A=A+x_i; B=B+x_i^2
A=A/n
B=(B/n-A^2)^0.5
obe maju rovnaku vypoctovu zlozitost ale ten druhy ma iba jeden cyklus. da sa to jednoducho prerobit na tu s n-1 v menovateli.
nikee.x napsal(a):
... Může to vůbec správně vyjít? ...
moze a aj vyjde
nikee.x napsal(a):
... Co si o tom myslíte, nenapsal to nějaký diletant? ...
nie
Offline
