Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Diofantická rovnice, důkaz neexistence řešení (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 08. 2013 16:43 — Editoval sugyman (26. 08. 2013 17:55)
Diofantická rovnice, důkaz neexistence řešení
Dobrý den, mám problém s rovnicí 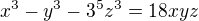 v oboru
v oboru 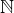
všechny proměné jsou po dvou nesoudělné a z je sudé. Potřebuju dokázat, že nemá řešení. Děkuji
BRKOS - matematický korespondenční seminář pro střední školy
Offline
- (téma jako vyřešené označil(a) sugyman)
#2 26. 08. 2013 21:28
Re: Diofantická rovnice, důkaz neexistence řešení
Dobrý deň. Môj postup nie je ani zďaleka elegantný, ale účel by to malo splniť.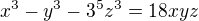
Vyriešením tejto rovnosti pre z, dostaneme (z wolframu). Môže sa to prekontrolovať, ale verím, že kubické rovnice zráta.
http://www.wolframalpha.com/input/?i=x% … E3%3D36xyz
- namiesto premennej z som použil 2z, keďže z má byť párne.
- uvažujeme len to prvé riešenie, lebo komplexné čísla nás momentálne nezaujímajú
Len prepíšem to čudo ... rozdelím ho na dva sčítance, lebo sa to zle prepisuje ...
![kopírovat do textarea $z_{1}=\frac{\sqrt[3]{2}xy}{9\sqrt[3]{-3x^{3}+3y^{3}+\sqrt{9x^{6}+14x^{3}y^{3}+9y^{6}}}}$](/mathtex/23/2355d40ecfe33b4e1700b24ba558563f.gif)
![kopírovat do textarea $z_{2}=\frac{\sqrt[3]{-3x^{3}+3y^{3}+\sqrt{9x^{6}+14x^{3}y^{3}+9y^{6}}}}{18\sqrt[3]{2}}$](/mathtex/2a/2afd612e75aa81a0ad070fd986124a13.gif)
Všimnime si, že menovateľ z_1 a čitateľ z_2 sú dosť podobné až na konštantu 9. Označme tú tretiu odmocninu (*).
Našim cieľom je nájsť prirodzené x,y tak, aby z bolo tiež prirodzené. To znamená, že keď pri prirodzených x,y dosiahneme, aby (*) bola nejaký prirodzený alebo celý násobok ![kopírovat do textarea $\sqrt[3]{2}$](/mathtex/e7/e77ed8d8f473e6819793afdd5a121307.gif) máme skoro vyhraté.
máme skoro vyhraté.
Napíšem, čo myslím:
Ak ![kopírovat do textarea $\sqrt[3]{-3x^{3}+3y^{3}+\sqrt{9x^{6}+14x^{3}y^{3}+9y^{6}}}=k\sqrt[3]{2}$](/mathtex/03/03a22702eadb9a84125e517e79973648.gif) , potom
, potom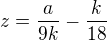 , kde a je nejaká rozumná konštanta (prirodzená).
, kde a je nejaká rozumná konštanta (prirodzená).
Teda otázka znie či platí:![kopírovat do textarea $\sqrt[3]{-3x^{3}+3y^{3}+\sqrt{9x^{6}+14x^{3}y^{3}+9y^{6}}}=k\sqrt[3]{2}$](/mathtex/03/03a22702eadb9a84125e517e79973648.gif)
Na to, aby to platilo potrebujeme, aby 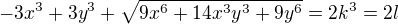 , no a k tomuto je potrebné, aby
, no a k tomuto je potrebné, aby 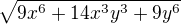 prirodzené číslo. A to je len vtedy ak to pod odmocninou je štvorec.
prirodzené číslo. A to je len vtedy ak to pod odmocninou je štvorec.
No a to štvorec nie je. Tým by sme mali skončiť, lenže práve ma napadlo, že som nerozobral možnosť, že to štvorec bude ak x alebo y bude nula.
Teraz ide o to či nulu považuješ za prirodzené číslo. Ak nie, tak sme hotoví. Ak áno treba ...
Offline
#3 27. 08. 2013 15:44
Re: Diofantická rovnice, důkaz neexistence řešení
↑ N3st4:
Ahoj, předpokládám, že jsi vycházel z tvaru  .
.
Jak ale můžu vědět, že pro nějaká vhodná 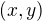 neexistuje takové
neexistuje takové 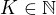 které splňuje rovnici
které splňuje rovnici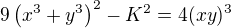 ?
?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#4 27. 08. 2013 16:18
Re: Diofantická rovnice, důkaz neexistence řešení
No pretože, keby také K existovalo platí: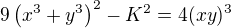
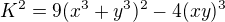
To znamená, že pravá strana musí byť štvorcom nejakého čísla (prirodzeného). No a jediná možnosť ako dostať na pravej strane štvorec z prirodzeného čísla je tá, že pravá strana je v tvare štvorca. A to je spor, lebo pravá strana nemôže byť štvorcom. Hlavnú váhu v tejto úvahe má to, že K musí byť prirodzené. Pri nejakom iracionálom čísle by tento argument neprešiel.
Môžno, keď sa to vezme z inej strany, tak je to jasnejšie. Jediný spôsob, kedy môže byť rozdiel dvoch celých čísel,
( ) štvorcom prirodzeného čísla je len vtedy, ak sa ten rozdiel dá napísať ako štvorec. (To je jasné.) Lenže v tomto prípade to nejde.
) štvorcom prirodzeného čísla je len vtedy, ak sa ten rozdiel dá napísať ako štvorec. (To je jasné.) Lenže v tomto prípade to nejde.
Dáva to zmysel?
Offline
#5 31. 08. 2013 20:22
- check_drummer

- Příspěvky: 4634
- Reputace: 99
Re: Diofantická rovnice, důkaz neexistence řešení
↑ sugyman:
Ahoj, kam jsem zatím dospěl (moc toho není):
"Máte úhel beta." "No to nemám."
Offline
#6 12. 09. 2013 21:25
Re: Diofantická rovnice, důkaz neexistence řešení
Tak můj učitel matiky (prof. Bulant) mi napsal, že jemu se to nepodařilo dokázat elementárně (kongruence apod.). Nicméně dokázal neřešitelnost rovnice pomocí její transformace na eliptickou křivku, o niz se pote
dokáže, že nemá žádné (netrivialni) racionalni body. Tímto to asi uzavírám :)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 13. 09. 2013 15:52
Re: Diofantická rovnice, důkaz neexistence řešení
Ahoj ↑ sugyman:,
Tak nam tu posli to tvoje riesenie co ti dal tvoj profesor.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 13. 09. 2013 20:33
Re: Diofantická rovnice, důkaz neexistence řešení
↑ vanok:
Profesor Bulant nám žádné řešení nedal, pouze to okomentoval se slovy, že elementárními prostředky se mu to vyřešit nepodařilo. Po převedení na eliptickou křivku pak dokázal, že rovnice nemá řešení.
Mimochodem, tato rovnice vznikla úpravou rovnice 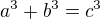 , což je "další" tvrzení zajišťující neřešitelnost zadané rovnice.
, což je "další" tvrzení zajišťující neřešitelnost zadané rovnice.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 13. 09. 2013 21:28
Re: Diofantická rovnice, důkaz neexistence řešení
Ahoj ↑ byk7:,
no ta druha moznost je pristupnejsia.
To naznacene riesenie ma zaujimalo, lebo podla mna,na pouzitie eliptickych kriviek je treba zvolit jednu z neznamych ako parameter, ktory potom popisuje "rodinu" eliptickych kriviek.
No ale v aritmetike je casto vela, a niekedy prekvapivych, rieseni.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Diofantická rovnice, důkaz neexistence řešení (TOTO TÉMA JE VYŘEŠENÉ)

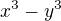 je dělielné 3 (dokonce 9) a 2 (dokonce 4) a navíc ani x ani y není dělitelné ani 2 ani 3 (spor s nesoudělností x,y,z). Navíc x=y (mod 3) a tedy x=6n+1,y=6m+1 nebo x=6n-1,y=6m-1 pro nějaká n,m.
je dělielné 3 (dokonce 9) a 2 (dokonce 4) a navíc ani x ani y není dělitelné ani 2 ani 3 (spor s nesoudělností x,y,z). Navíc x=y (mod 3) a tedy x=6n+1,y=6m+1 nebo x=6n-1,y=6m-1 pro nějaká n,m.