Matematické Fórum

Blackflower · 14. 09. 2013 13:11

Ahojte,
mám teleso dané rovnicami: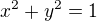
$x^2+y^2=1$
$x^2+y^2=4$
$z=1$
$x+y-z+4=0$
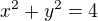
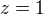
Cez prázdniny som všetko pozabúdala a neviem určiť medze. Vedel by mi niekto pomôcť?

Brano · 14. 09. 2013 14:21

odporucam cylindricke suradnice
$x=r\cos\varphi$
$y=r\sin\varphi$
$z=z$
prve dve hranice ti daju $r\in[1,2]$ a $\varphi\in[0,2\pi]$
a druhe dve
$z\in[1,4+r(\cos\varphi+\sin\varphi)]$ - vsimni si, ze minimum toho druheho clena je $4-2\sqrt{2}>1$

Rumburak · 14. 09. 2013 14:23

Ahoj. Na "meze" je ještě brzo. Začni tím, že si ujasníš množinu v R2 ohraničenou křívkami o rovnicích

$x^2+y^2=1$ , $x^2+y^2=4$ .

Blackflower · 17. 09. 2013 11:27

Vďaka obom za rady.
↑ Rumburak: To som ešte zvládla, že je to medzikružie... len potom som mala problém dať to do 3D, ani nakresliť v programe som to nevedela.
↑ Brano: Takže teraz mám integrovať iba determinant transformácie (ten mi vyšiel $r(\cos \varphi -\sin \varphi )$ ) s hranicami, ktoré si napísal?

Eratosthenes · 17. 09. 2013 12:11

↑ Blackflower:

To ne, ještě je tam ta rovina

$x+y-z+4=0$

Blackflower · 17. 09. 2013 12:13

↑ Eratosthenes: Tak som potom asi zle pochopila, čo napísal Braňo... myslela som, že to sa premietne iba do hraníc...

Jj · 17. 09. 2013 12:43

↑ Blackflower:

Snad se nepletu, ale myslím, že uvažujete správně. Jen má být |determinantu| a nejsem si jistý, zda je determinant transformace spočítán správně.

Blackflower · 17. 09. 2013 12:45

↑ Jj: Mohla som sa pomýliť... tiež sa mi to celkom nezdá, lebo výraz, čo mi vyšiel, môže byť pre niektoré hodnoty kladný a pre niektoré záporný...

Brano · 17. 09. 2013 22:56

rovnica $x+y-z+4=0$ je samozrejme zaratana v tych medziach co som napisal - v tej hornej pre $z$
objemovy element je $rdrd\varphi dz$ , alebo inymi slovami Jakobian transformacie je iba $r$

Matematické Fórum

#1 14. 09. 2013 13:11

Objem telesa

#2 14. 09. 2013 14:21

Re: Objem telesa

#3 14. 09. 2013 14:23

Re: Objem telesa

#4 17. 09. 2013 11:27

Re: Objem telesa

#5 17. 09. 2013 12:11

Re: Objem telesa

#6 17. 09. 2013 12:13

Re: Objem telesa

#7 17. 09. 2013 12:43

Re: Objem telesa

#8 17. 09. 2013 12:45

Re: Objem telesa

#9 17. 09. 2013 22:56

Re: Objem telesa

Zápatí