Matematické Fórum

foxer · 20. 09. 2013 21:07

potrebujem objasnit či spráne rozumiem čo znamená surjektivna funkcia
rozumiem správne definicii surjekcie že každé y z kartezianskej sústavy suradnic má priradenú aspoň jednu hodnotu x?? takže
funkcia $y=x^{1/2}$ neni surjektivna lebo pre y<0 nemá priradene žiadne x
funkcia 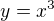$y=x^{3}$ je surjektivna lebo H(f)=R
funkcia $y=x^{2}$ neni surjektivna

Je jasne že funkcia musí byť injektívna(prostá) aby k nej existovala inverzna funkcia ale prečo musí spľnať aj surjekciu?

Andrejka3 · 20. 09. 2013 21:45

Ahoj.
Fce / zobrazení je zadáno tehdy, známe-li odkud přiřazuje (obor), kam přiřazuje (nazvěme to kooborem) a jak (předpis).
Zobrazení $g:\;A\rightarrow B$ je surjektivní právě když $g(A)=B$ , kde definujme pro $X\subset A$ obraz množiny jako
$g(X)=\{g(x);\;x \in X\}$ (bylo by lepší značení jako například $g_*X$ ).

Například
$f:\; \mathbb{R}\rightarrow \mathbb{R},\; x\mapsto x^2$ není surjekce, neboť $f(\mathbb{R})=\mathbb{R}^+\cup\{0\}$ . Kdezto
$g:\;\mathbb{R}\rightarrow \mathbb{R}^+\cup\{0\},\; x\mapsto x^2$ je surjekce, protože obraz oboru v $g$ je koobor $g$ .

Ohledně inverze, rozlišujeme fci, jež je invertibilní zprava, fci jež je invertibilní zleva, a oboustranně invertibilní.

$f:\;A\rightarrow B$ je invertibilní zleva, právě když existuje fce $g:\;B\rightarrow A$ taková, že
$gf=1_A$ .
Fce je zleva invertibilní, právě když je prostá (injekce).

Kde $1_A$ značí zobrazení $A\rightarrow A$ , $a\mapsto a$ (identita na $A$ ).

$f:\;A\rightarrow B$ je invertibilní zprava, právě když existuje fce $h:\;B\rightarrow A$ taková, že
$fh=1_B$ .
Fce je zprava invertibilní, právě když je na (surjekce).

Fce $f$ je oboustranně invertibilní, právě když je invertibilní zleva a je invertibilní zprava.

byk7 · 20. 09. 2013 21:55

Uvažme funkci $f:\mathsf{X\to Y}$ . Aby $f$ byla surjektivní, musí být použita celá množina $\mathsf Y$ .
Nechť je $f:x\mapsto\sqrt x$ a volme
1) $\mathsf{X=Y}=\mathbb{R}$ , tato funkce není surjektivní, protože $\exists y\in\mathbb{R}^-$ , že neexistuje (v $\mathbb{R}$ ) $x$ takové, pro které by platilo $f(x)=y$ ,
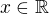2) $\mathsf X=\mathbb{R},\,\mathsf Y\subseteq\mathbb{R}^+\cup\{0\}$ ( $\mathsf Y$ je libovolná podmnožina nezáporných čísel) tentokrát $f$ bude surjekce, protože pro každé $y\in\mathsf Y$ dokážeš najít $x\in\mathbb{R}$ splňující $f(x)=y$ .

K tvému dotazu o existenci inverzní funkce -- injektivnost ti zaručí, že $\not\exists y$ takové, že pro $x_1\neq x_2$ by platilo $f$x_1$=f$x_2$=y$ , surjektivnost ti zas dá, že $\forall y\ \exists x:f(x)=y$ . Zkombinováním těchto dvou podmínek dostáváš, že pro každé $x$ existuje právě jedno $y$ splňující $f(x)=y$ , tímto máš dánu jednoznačnost přiřazení, tj. pokud znáš $x$ můžeš dopočítat $y$ a zpětně, pokud znáš $y$ , můžeš spočítat jemu odpovídající $x$ .
Pokud je funkce injektivní a surjektivní, říkáme, že je bijektivní. A pokud je funkce bijektivní, pak k ní existuje inverze. :-)

Snad jsem to v závěru nenapsal moc zmateně.

P.S.: Vidím, že jsem byl předběhnut, no, když už jsem si dal tu práci, tak to tu nechám.

Andrejka3

↑ byk7:
Myslím, že je dobře, žes odpověděl. Vůbec jsem nepsala, co je vlastně inverzní fce.
Doplnila bych jen k mému textu,

Andrejka3 napsal(a):
$f:\;A\rightarrow B$ je invertibilní zleva, právě když existuje fce $g:\;B\rightarrow A$ taková, že
$gf=1_A$ .
Fce je zleva invertibilní, právě když je prostá (injekce).

fci g se říká levá inverzní k f.

Andrejka3 napsal(a):
$f:\;A\rightarrow B$ je invertibilní zprava, právě když existuje fce $h:\;B\rightarrow A$ taková, že
$fh=1_B$ .
Fce je zprava invertibilní, právě když je na (surjekce).

fci h se říká pravá inverzní k f.

Dále, pokud existuje pravá inverzní i levá inverzní (značme je stejně jako předtím), pak je
$g=g\circ 1_B = g(fh)=(gf)h=1_A \circ h=h$ , tedy je každá levá inverzní zároveň pravou inverzní, a je jednoznačně určená (jedinečná). Říká se jí (oboustranně) inverzní fce k fci f.
Ta tedy existuje, právě když je f bijekce (viz kolega ↑ byk7:).

foxer · 21. 09. 2013 10:24

tak ešte pre kontrolu k mojej trojicii fcii
na $\mathbb{R}->\mathbb{R}$ je surjektivna len 2. fce
na $\mathbb{R}->\mathbb{R^{+}}\cup \{0\}$ sú všetky surjektívne
na $\mathbb{R}->\mathbb{R^{+}}\cup \{0\}$ sú všetky bijektívne?

Andrejka3

↑ foxer:

foxer napsal(a):
na $\mathbb{R}->\mathbb{R}$ je surjektivna len 2. fce

1. Jak definuješ 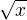$\sqrt{x}$ pro $x<0$ ?
2. je sur, 3. není sur.

foxer napsal(a):
na $\mathbb{R}->\mathbb{R^{+}}\cup \{0\}$ sú všetky surjektívne

1. Jak definuješ 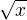$\sqrt{x}$ pro $x<0$ ?
2. taková restrikce neexistuje. Kolik je $(-1)^3$ ? Je výsledek v kooboru fce?
3. je sur

foxer napsal(a):
na $\mathbb{R}->\mathbb{R^{+}}\cup \{0\}$ sú všetky bijektívne?

1. Jak definuješ 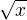$\sqrt{x}$ pro $x<0$ ?
2. taková restrikce neexistuje. Kolik je $(-1)^3$ ? Je výsledek v kooboru fce?
3. Opravdu je prostá? Kolik řešení má rovnice $x^2=1$ například.
Edit: Můžeš úžit i obor fcí: Například, je $f:\; \mathbb{R} \rightarrow \mathbb{R}^+\cup\{0\},\;f(x)=x^2$ bijekce? Je bijekce její restrikce,
$g:\;\mathbb{R}^+\cup\{0\}\rightarrow \mathbb{R}^+\cup\{0\},\;g(x)=x^2$ ? Je bijekce restrikce $f$ na jiný obor:
$h:\;\mathbb{R}^-\cup\{0\}\rightarrow \mathbb{R}^+\cup\{0\},\;h(x)=x^2$