Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Ostatní
- » vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
#26 19. 09. 2013 10:13 — Editoval buff (19. 09. 2013 10:14)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Jelena byla zase rychlejší, zrovna jsem doplňoval příspěvek, takže to pošlu nanovo:
Mám ten trojúhelník SPD (podle Bradova pojmenování SPD ... Střed - První vrchol - Druhý vrchol ) např. s úhlem 60° rozdělit na dva trojúhelníky, abych získal pravé úhly? Je to správný postup? Myslím tím, že nově vytvořenž přímka bude protínat střed přímky PD (tj. přímka začínající na prvním a končícím na druhém vrcholu).
PS: pozice vrcholů si spočítat umím
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#27 19. 09. 2013 10:17 — Editoval buff (19. 09. 2013 10:18)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
OK, tak asi použiju ten vzorec na výpočet vzdálenosti dvou bodů.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#29 19. 09. 2013 10:34
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Takže tak
Code:
vertex1 := getCircleXYCoords(0, radius) vertex2 := getCircleXYCoords(360/sides , radius) ; side_length := Sqrt( (a1-b1)^+(a2-b2)^ ) side_length := Sqrt( (vertex1["x"]-vertex1["y"])^+(vertex2["x"]-vertex2["y"])^ )
Naštěstí ten vzorec je docela snadno zapamatovatelný.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#30 19. 09. 2013 11:17 — Editoval buff (19. 09. 2013 11:30)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
OK, tak dostal jsem délku strany, např 3. Vydělím 4 a zaokrouhlím nahoru, takže dostanu 1. Když tuto hodnotu "zakreslím" na stranu PD, zleva, vznikne mi průsečíík. Když bych to znázornil na hodinách tak P je 0 (dvanáctá hodina), hodnota 1 je první hodina, a 3 je vrchol D. Jak zjistím úhel mezi 12 a první hodinou?
Edit:
To asi byla zbytečná otázka. 90*1/3 = 30 ...
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#31 19. 09. 2013 11:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
↑ buff:
Jelikož trojúhelník PDS je rovnoramenný se známým úhlem u středu (úhel PSD), můžeš také dopočíst úhly u základny PD (180-(360/počet stran))/2. Potom pomocí kosinové věty dopočíst stranu S1 a pomocí sinové věty dopočteš sinus úhlu oproti straně P1.
Jiná možnost je přes odchylku vektorů SP a S1, pokud jde stanovit souřadnice bodu (1) - což jde a je rychlejší.
Edit:
To asi byla zbytečná otázka. 90*1/3 = 30 ...
To nemyslím, pokud vydělíš stranu základny 4, tak dostaneš přesnou hodnotu délky čtvrtiny strany a tomuto dělení nebude odpovídat dělení úhlu na 4 stejné díly (a 90/3 neodpovídá dělení strany na stejné 3 díly). Také pozor na zaokrouhlování. Už vidím riziko, že se v tom zamotáš/zamotáme :-)
Proč ten úhel potřebuješ?
Offline
#32 19. 09. 2013 13:29
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Asi ho nepotřebuju. Ještě si nejsem úplně jistý. Zatím se snažím najít nějaké vodítko jak vypočíst určitou toleranci aby ty případné věže nebyly moc blízko a aby tam nějaká zbyla. Pod pojmem věž si představuj ty krokované souřadnice.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#33 19. 09. 2013 16:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
↑ buff:
Jednotlivé rozměry - celé opevnění, tloušťka stěny, velikost věže - to je nějak úměrně sobě upravovováno, může být úměrně zvětšeno/zmenšeno?
Proč tak zakládáš na krokování pomocí úhlu - je snad uvnitř opevnění nějaké zbraň, která se jen otáčí? Není přeci jen pohodlnější pracovat se souřadnici všech bodů stěny, pokud máš rovnici přímky stěny?
Věž má větší obrannou hodnotu, než jen zeď a na postavení věže je třeba mít nějaké předpoklady (ekonomické - body, bonusy)?
Pokud rozměr věži (řekneme "rozměr podél stěny") je pevně dán, potom maximální počet věží je (délka stěny)/(rozměr věží) zaokrouhleno na celé číslo dolu. A od tohoto čísla můžeš počet věží snižovat do 0 a navyšovat velikost mezer. Stavitel dostavuje stěnu postupně, nebo mu "vyroste" celá stěna i s věži?
Offline
#34 19. 09. 2013 18:56
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
To generování je jedodušší když je to na základě kruhu a krokování po stupních. Stačí na to jeden matematický vzorec. Určování vdálenosti kolem vrcholů je věc jiná. To je navíc. Tloušťka stěny se nemění, ale uvažoval jsem o té možnosti že bych vytvořil třeba dvojité stěny záměrně, aby bylo masivnější opevnění. To ale není aktuální a nebyl by to žádný problém. Uživatel nemusí zadávat odkud jam bude stěna vést, prostě jen zadá poloměr a je to.
Počet věží je dán za prvé tím jak velké je krokování, nikoliv délkou stěny. Za druhé počet věží může být snížen v případě force_vertex=1 tak, že věž která je moc blízko vrcholu se nevytvoří.
Připravuji si ty hodnoty, které určují ty vzdálenosti kdy je věž moc blízko, decision_point. Ale bude to až zítra možná později. Musím si to nakreslit na čtverečkovaný papír.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#35 20. 09. 2013 09:55
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Existuje nějaká stránka kam bych mohl zadat (nejlépe zkopírovat nebo naimportovat hodnoty pro graf a následně je vyobrazit? Případně, to by byl velký bonus, kdyby byla schopná zjistit podle jakého vzorce se to řídí.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#36 20. 09. 2013 11:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
↑ buff:
Zdravím,
pro takový první náhled bych používala grafy v EXCELu nebo v CALCu - používáš? Umožní také proložit přes data přímku nebo křivku a udělají odhad závislosti (vytvoří vzorec), ale je to jen odhad chování dat, nějaký trend - pohledej "Regrese". Něco od pohledu na graf se dá vytvořit i ručně (z určitých zkušenosti)
Obdobnou funkci máš ve WA - bez psaní žádných kódů, jen vložit data - zde chce prozkoušet, jakou závislost očekáváš, zda přímku nebo některou křívku. omezeně i v MAW (Lagrange a metodu nejmenších čtverců), v maxima např. již kód musí být napsán.
Stačí tak na úvod?
Offline
#37 20. 09. 2013 12:14 — Editoval buff (20. 09. 2013 15:32)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Bude to přímka, která postupně stoupá, ale není lineární a končí v určitém bodě, protože se jedná o přímku a krokování je menší nebo rovno délce přímky.
Představ si graf a na dolní ose je veličina l určující vzdálenost. l=2 znamená, že každá prvá věž je vynechána. Na grafu l navyšuju vždy po jedné.
Na grafu (který si představíš) je zachycena křivka vztahující se k určitému poloměru r.
Výsledná hodnota je decision_point neboli počet kachlí/bodů, od vrcholu, které se nebudou zpracovávat/zobrazovat.
Zatímco při malém poloměru r je výsledná hodnota pro r=2 nejdříve 0, pak pro r=3 jsou výsledné hodnoty 0,1,1,0 . Pak pro r=4 jsou hodnoty 1,1,1,1,1, pro r=5 jsou hodnoty 2,2,2,2,2,2,2,1 ... Pak od l=3 pro r=6 jsou hodnoty 2,2,2,3,3,3,3,3 (tzn. až do maximální hodnoty l je maximální hodnota 3) dále pro r=8 od l=3 je to 2,2,3,3,3,3,4,4,5,6 . pro r=9 a od l=3 je to 2,2,2,4,3,4,3,4,4,4,5, pro r=10 od l=3 je to 2,2,3,3,4,4,4,4,6,6,7,7,7 pro r=11 od l=3 je to 2,2,3,3,4,4,4,5,4,7,8,8,8,8,8,8
r=12 výše nemám dokončené. Mohu zapsat do tabulky až budu hotov
Souvislost kterou v tom vidím - tři faktory.
Střed či prostředek mezi hodnotami (l) odkud se to jakoby duplikuje s tím rozdílem, že od středu směrem k l níže hodnoty klesají a od středu l výše, hodnoty stoupají.
Lépe by bylo zobrazit to na grafu a střed vyznačit.
Další dva faktory je horní a dolní hranice.
Třetí faktor je horní hranice pro decision_point, která je tu proto, aby v prostředku stěn zůstalo nějaké místo na vykreslování/zpracování některých bodů. Proto se výsledné hodnoty závěrem opakují.
edit:
A ještě jeden podstatný faktor je ten, že jak zvětšuješ radius, tak se ty výsledné hodnoty postupně ustálují, tzn. že už se pak nemění (od určité hodnoty l. Tam bych měl vysledovat souvislost mezi l a r z tohoto pohledu, abych mohl definovat kdy je třeba spočítat hodnotu l.
edit 2 - klíč k řešení:
Musím nejdříve vypočítat rozdíl u stabilizovaných hodnot. př. stabilní hodnota pro d=12 je (zřejmě) 6. 6 je 50% z 12. Pro d=11 je stabilní hodnota 6. Kolik procent je 6 z 11? 54,54 perioda procent. Stabilní hodnota pro d=10 je 5 => 50%. Stabilní hodnota pro d=9 je 5. Kolik procent je 5 z 9? 55,5 perioda %. Pro d=8 je to 4 tj. 50%. Pro d=7 je to 4. Kolik procent je 4 z 7? 57,142857 perioda procent. U 6 je to opět 3, 50%. U d=5 je to 3. Kolik procent je 3 z 5? 60 procent. U 4 je to 2, tedy opět 50%. U d=3 je to 2. Kolik je to procent? 66,6 perioda procent. 1 je stabilní od d=1.
Takže u lichých čísel je to kolem (oprava) 58,78%, u sudých 50% Ovšem když se blížíme ke středu kružnice - čím menší je poloměr, tím menší bude decision_point l => čím menší r, tím je výsledek méně procent ze vzdálenosti d Toto ale platí pouze pro čtyřúhelník!
Čím více stran bude polygon mít, tím více bude mít věží na vrcholech, takže o to více musíme toto číslo zmenšit!
Řešení?
bude záviset jestli stabilní hodnota pro vzdálenost l je +/- "něco" větší nebo menší než délka strany.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#38 20. 09. 2013 13:44 — Editoval jelena (20. 09. 2013 13:47)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
↑ buff:
děkuji, s terminologii ještě trochu potíž - pokud přímka, tak je lineární funkce. Jinak není. Přímka, která má konečnou délku, je úsečka.
veličina l určující vzdálenost. l=2 znamená, že každá prvá věž je vynechána. Na grafu l navyšuju vždy po jedné.
to si ještě neumím představit. Z Tvého popisu by odvodila takové závěry:
r - poloměr kružnice opsané čtverci,
a - délka strany čtverce, 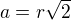 ,
,
w - "podélný rozměr" věže, tedy ten, který je podstatný pro umístění na stranu.
Pro zaokrouhlení směrem dolu na celé číslo používám funkci floor (dolní celá část) a nejdřív výpočtu maximální počet věží W:  (na ukázku jsem zvolila podélný rozměr w=3, tedy až do r o něco více, než 2 ještě žádnou věž nezakreslíš, potom počty věží vidíš na ose y - odpovídají tomu vodorovné čáry. Ve vzorci můžeš měnit to číslo místo 3 a dívat se, co děla výsledek).
(na ukázku jsem zvolila podélný rozměr w=3, tedy až do r o něco více, než 2 ještě žádnou věž nezakreslíš, potom počty věží vidíš na ose y - odpovídají tomu vodorovné čáry. Ve vzorci můžeš měnit to číslo místo 3 a dívat se, co děla výsledek).
Počítám velikost mezery m: 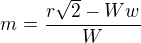 , pokud tato mezera je větší, než Tebou stanovená hranice (to je to povídání o procentech, stabilitě, to se musíme dohodnout na kriterii), tak snižuji hodnotu W o 1 a opět kontroluj velikost mezery. V prvním kroku po snížení, mám
, pokud tato mezera je větší, než Tebou stanovená hranice (to je to povídání o procentech, stabilitě, to se musíme dohodnout na kriterii), tak snižuji hodnotu W o 1 a opět kontroluj velikost mezery. V prvním kroku po snížení, mám 
Je to pro Tebe použitelné? Já nejspíš nebudu mít teď čas, snad jen nahlédnu, uvidíme, co bude požadovat okolí :-).
Offline
#39 20. 09. 2013 14:03 — Editoval buff (20. 09. 2013 14:09)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Jelena:
Nevím jestli si dočetla ty moje závěry o stabilních hodnotách, které jsem přidal do příspěvku. Radši zkontroluj. Konečně mám něco čeho se mohu chytit.
Tam rozměr věže nehraje roli. Když tak počkej až dodělám ty hodnoty a já to pak hodím do tabulky a do grafu.
Délku strany znám, tu jsem už počítal a nepamatuji si jestli jsem to tu uváděl, ale v kódu ji mám.
Co se týče vzdálenosti mezi věžemi, tak to mám dojem že už taky znám a mám vypočítáno. Nebo možná nemám ale já to beru jako délka strany děleno počet věží na straně. Tedy délka strany děleno počet bodů, které bych měl aplikovat pokud bych to neomezil.
PS: Zatím jen analyzuju abych našel nějaké souvislosti a cesty k řešení, ale jasnější ti snad bude až dám ten graf.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#40 20. 09. 2013 14:29
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
↑ buff:
A nelíbilo by se ti třeba to dělat takto?
Offline
#41 20. 09. 2013 14:55 — Editoval buff (20. 09. 2013 15:24)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Honzc, tak to je bombovní! Něco takového bych sice chtěl, jenže prakticky je problém v tom, že ten program zvládá jen násobky 45° úhlů a ostatní nevypadá hezky. Ale třeba by se to taky nějak využilo. Já jsem původně chtěl taky nějaké útvary které mají takový tvar jak ty ukazuješ na těch modrých hvězdicích, ale zdálo se mi to moc složité, resp. nevěděl jsem jak na to. V podstatě, mě by zajímala ta poslední modrá hvězdice, protože ta splňuje pravidlo 45°! Taky jsem chtěl v budoucnu dělat program na výpočet podle vzdáleností jak je zadáváš ty. Takový program mám už rozdělaný, ale když dáš kód jak to udělat, tak ty červené polygony použiju v tom druhém programu. Pro účely aktuálního programu bych mohl ještě použít tu předposlední modrou hvězdici, kdyby se tam dal nějak nastavit ten úhel na 45°. To by se asi musela změnit délka strany která tvoří "vrchol".
Ještě by bylo fajn kdybych pak mohl rozhodnout o tom jaké věže chci dát na vnější rohy a jaké na vnitřní. Je tam možnost použít dva až tři typy věží, případně bych mohl na vnitřní rohy umístit brány.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#42 20. 09. 2013 18:04 — Editoval buff (21. 09. 2013 20:34)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Pokoušel jsem se to nahrát online ale konverze trvá nějak dlouho a zatím se to nezobrazilo, takže mezitím ti to posílám sem:
Aktualizováno - soubor nyní obsahuje grafy s regresivní křivkou odchylky od stabilních hodnot
http://ulozto.cz/xHBSuLNf/decision-point-zip
Podotýkám:
Levý sloupec tučně vyznačuji "prostředek"
Pravý sloupec tučně černě vyznačuji anomálie a tučně červeně stabilizované hodnoty po ustálení. Poslední křivka v listě r12 ukazuje všechny hodnoty po ustálení. Pak platí to pravidlo které jsem zvýraznil červenou barvou výše.
Nyní nutno vyřešit jak vygenerovat takovou křivku a pak tu druhou věc, jakým procentem to snížit pokud se změní poměr mezi těma hodnotama (o tom jsem psal v tom červeném odstavci).
Jdu odpočívat a když tak to zítra dořešíme. Ráno a dopoledne bývám "plodnější".
Honza:
Tu funkci až ji budeš mít, prosím, budeme řešit až dořeším tuhle věc.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#43 20. 09. 2013 23:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
buff napsal(a):
Nevím jestli si dočetla ty moje závěry o stabilních hodnotách, které jsem přidal do příspěvku. Radši zkontroluj.
něco bylo v průběhu, jak jsem psala a dívala na Náhled, zbytek + graf jsem teď dočetla. Zodpovědně prohlašuji, že jsem nic nepochopila :-)
↑ Honzc:
:-) pěkné, jen opatrně s nekonvexními útvary - z fortifikačního hlediska nejsou ideální (to určitě i sám odvodíš). Lepší jsou konvexní a na rozích takové předsunuté výstupky - např. jak má kolega na mapě, co již umísťovat.
Zdravím a zdárné budování přeji (nejlépe beze mne), děkuji.
Offline
#44 21. 09. 2013 09:00
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Ke grafu:
Neuměl jsem ten graf udělat tak, aby byla zobrazena ta modrá osa dole, takže se to zobrazilo jako modrá křivka. Což ale není na obtíž.
Nevím co k tomu dodat.
Graf zobrazuje červenou křivku průběhu toho decision_point, což je vzdálenost od vrcholu.
Stabilní hodnota proměnné decision_point je ta, která se už ustálila a nebude se při navyšování poloměru dále měnit.
Graf na listu r12 zobrazuje křivku, kdy při poloměru r=12 a s určitou vzdáleností d mezi věžemi, dostáváš vzdálenost decision point, do které se nebudou body zahrnovat do výsledku.
Jsou dvě možnosti jak dosáhnout výpočtu decision_point. Buď to budu počítat jako procento ze vzdálenosti d, nebo pomocí jiného vzorce. Ale zdá se, že pro mě je nejjednodušší ta první metoda. Poté porovnám číslo s poloměrem a pokud je výsledek větší než je výsledek funkce, kterou musím teprve vytvořit a jejích vstupním parametrem je radius a délka strany, pak musím ten první výsledek upravit tak, aby výsledek byl rovný nebo menší než výsledek další funkce .... tohle není dokončené, protože ty "funkce" neboli matematické postupy/algoritimy budu tvořit dneska.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#45 21. 09. 2013 10:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Graf na listu r12 zobrazuje křivku, kdy při poloměru r=12 a s určitou vzdáleností d mezi věžemi, dostáváš vzdálenost decision point, do které se nebudou body zahrnovat do výsledku.
určitá vzdálenost mezi věžemi se počítá jak? Můžeš mi, prosím, celý proces, který jsi popsal v příspěvku 37 a 44 ukázat na příkladu - viz obrázek (poloměr opsané kružnice je 12, strana čtverce je  (cca). Děkuji, absolutně to nespěchá.
(cca). Děkuji, absolutně to nespěchá.
Offline
#46 21. 09. 2013 10:47 — Editoval buff (21. 09. 2013 10:49)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Jj, moment. Už začínám psát kód.
Tady je první výpočet.
Code:
distance_wt := floor(side_length/stepSize) ; kolikáté pole je obsazeno věží ; Init variables of this circle distance_reduction_percent:=mod(distance_wt,2)?50:58.78 ; stable values of decition_point are 50% of distance_wt . Odd values are about 58.78% but the bigger radius, the clost to 50%. The less radius, the more than 58.78%
distance_wt je ta vzdálenost mezi věžemi. Nevěděl jsem jak to pojmenovat, tak takto. Vzdálenost mezi věžemi není přesný popis. Přesněji: kolikáté pole je obsazeno věží. Čily kolikátá věž je první věž, když v počáteček je 0. Pokud distance_wt=5 tak tedy na pátém bodě bude věž. nejsnadnější je vzít si čtverečkovaný papír a nakreslit si čtverec na papíře. každá strana má např. 9 políček. 0 chápu jako uhlopříčku, 1. a 2. políčko strany je prázdné a na třetím je věž. Tedy distance_wt=3.
Co teď potřebuju je udělat opravu distance_reduction_percent podle té poznámky která tam je o lichých číslech
PS:
Předem se omlouvám pokud to bude trvat, pracuji pomalu, nejsem v kondici.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#47 21. 09. 2013 11:09 — Editoval buff (21. 09. 2013 11:15)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Považuji za lepší než na kružnici použít jako pomůcku čtverečkovaný papír jestli souhlasíš.
Bude ti stačit můj slovní popis na čtvercovém papíře?
Jo, udělal jsem asi menší chybu v poloměru, ale to nehraje roli. Na tom čtverci to s čím pracuji vlastně není poloměr kružnice opsané, ale vzdálenost od středu kružnice ke středu strany! No, to nevadí, to nehraje roli ve výsledku. Výsledek je stejně určen tou délkou strany.
Tedy zeleně jsem vytáhl ty čtverce, které představuji obvod našeho čtverece. Modře jsou pak věže, které mají rozestup distance_wt
Statistiky jsem dělal na základě tohoto diagramu.
Chyba:
Code:
distance_wt := round(side_length/stepSize)
Vlastně to nemohu použít protože stepSize je ve stupních
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#48 21. 09. 2013 11:21 — Editoval buff (21. 09. 2013 11:58)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
jelena napsal(a):
↑ buff:
r - poloměr kružnice opsané čtverci,
a - délka strany čtverce,,
w - "podélný rozměr" věže, tedy ten, který je podstatný pro umístění na stranu.
w nebude hrát roli (to jsem už psal).
Co je ale odmocnina ze dvou? A jaktože ve vzorci není počet stran? Neměl by výpočet zohledňovat že může jít o polygon? Jak jinak vypočítat ty rozestupy věží? Rozestup na mém kostičkovaném diagramu je distance_wt = 3 . Protože zakresluju každou čtvrtou věž.
Jak budu vědět jak spočítat tu vzdálenost distance_wt, tak zas budu moci pokračovat ve výpočtu, ale tady jsem se zasekl. Nějak jsem si neuvědomil, že distance_wt počítám špatně.
To hlavní co hraje roli ve výsledku je délka strany kolik stran má polygon - protože čím bude strana kratší tím méně věží tam mohu dát.
PS:
Asi jsem do toho vnesl chaos díky tomu že jsem špatně pojmenoval tu vzdálenost od středu kruhu ke středu strany :-( místo r jsem měl dát něco jiného.
PS2:
Bohužel nevím jak na kalkulačce ve Windows spočítat odmocninu ze dvou.
PS3:
O tom jak počítám délku strany jsme se už bavili. Nepočítám to jako ty, ale výsledek mám stejný jako ty.
Toto je výpočet bez zaokrouhlení
Code:
sideLength := Sqrt( _Power(vertex1["x"]-vertex1["y"]) + _Power(vertex2["x"]-vertex2["y"]) )
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#49 21. 09. 2013 12:19 — Editoval buff (21. 09. 2013 12:53)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Hele, já mám pocit, že už opravuju věci, které byly původně dobře a zase z nich dělám chyby.
Je tenhle výpočet dobře?
PŘÍKLAD 1:
distance_wt = side_length/stepSize = 17 / 5 = 3.4
distance_wt = roundMe(3.4) = 3.5 (platná hodnota pro program, která říká že věž budu umísťovat do středu kachle)
KONTROLA:
360/sides/stepSize = 360 / 4 / 5 = 90 / 5 = 18
90/18 = 5
PŘÍKLAD 2:
distance_wt = side_length/stepSize = 17 / 7 = 2.42
distance_wt = roundMe(3.4) = 2.0 (platná hodnota pro program, která říká že věž budu umísťovat do středu kachle)
KONTROLA:
360/sides/stepSize = 360 / 4 / 7 = 90 / 7 = 12,8...
90/12,8.. = 7
ZÁVĚR:
Je jedno jestli dělím úhel 90° počtem kroků ve stupních, nebo dělím délku počtem kroků ve stupních, vždycky dostanu stejnou vzdálenost. Nechápu to, je to divné, ale vychází mi správný výsledek. Nevím zda by vycházel i u vícestranného polygonu. Ale asi jo. Samozřejmá podmínka je, že stepSize nesmí být větší než 360/sides = 90°
Edit:
Jo, musí to být správně. StepSize říká v podstatě kolik věží bude v tom úseku, je jedno jestli si pod tím představíš výseč ve tvaru dortu nebo úsečku jakožto stranu polygonu. Moje původní myšlenkové procesy byly správné, jenže občas je znovu pochopit je potíž (a to nemusí být ani tak velký časový horizont, abych zapomněl co jsem tím kódem původně myslel). Dělitel stepSize není závislý na poloměru.
Edit2:
Stejně ten zmatek co jsem tu vytvořil kolem r. To r má být asi zakreslené jako poloměr kružnice opsané. Jak říkám, dneska nejsem v kondici. Jsem unavený a vůbec mi to nemyslí. Velikost poloměru kružnice opsané ale nehraje roli při tom výpočtu distance_wt, protože ta už vychází z délky strany vypočítané ze souřadnic...
Edit3:
Měním tedy pojmenování pro ty sešity. Nikoliv r, ale rx.
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
#50 21. 09. 2013 16:16 — Editoval buff (21. 09. 2013 16:42)
Re: vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu
Mám hotové stabilní hodnoty pro rx=12
na případné matematické nedostatky kódu a jeho zjednodušení mě můžeš upozornit:
Code:
side_length := round(Sqrt( _Power(vertex1["x"]-vertex1["y"]) + _Power(vertex2["x"]-vertex2["y"]) )) distance_wt := round(side_length/(side_length/stepSize)) ; kolikáté pole je obsazeno věží distance_reduction_percent := 50 + ( mod(distance_wt,2)?50/distance_wt:0 ) ; stable values of decition_point are 50% of distance_wt . Odd values are about 58.78% but the bigger radius, the clost to 50%. The less radius, the more than 58.78% if ( distance_wt > 4 ) decision_point := decision_point-decision_point/100*distance_reduction_percent ; reduction of decision_point
Nyní budu řešit jak snížit hodnotu decision_point když snížím průměr kružnice (zmenším polygon).
Edit:
V podstatě jde o to, že mezi stabilní hodnotou a tou hodnotou při rx<=12 je nějaká odchylka, která se řídí pravidlem: čím větší je rx a čím větší je distance_wt, tím větší je decision_point. Platí ale decision_point<=8 .
Dobré na ukládání dokumentů, aby byly přístupné ke čtené online *.doc, *.rtf aj. http://www.viewdocsonline.com
Offline
- Hlavní strana
- » Ostatní
- » vytvoření podmínek pro správné polohy vrcholů pravidelného polygonu

