Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 23. 09. 2013 07:48
Re: Důkaz indukcí
↑ Mirgeee:
Dovolím si jen malou nápovědu - zkus se podívat na důkaz, že je prvočísel nekonečně mnoho. Mělo by tě to inspirovat;-)
Доктор сказал «в морг» — значит в морг!
Offline
#4 23. 09. 2013 14:16 — Editoval Brano (23. 09. 2013 14:29)
Re: Důkaz indukcí
↑ Mirgeee:
mas pravdu - nemusis ju v tej technike pouzit. ale kedze ziaden elegantny dokaz vyuzivajuci indukciu ma nenapada, tak mozes tento rozsirit na dokaz indukciou, tak ze tam pridas dve zbytocne vety:
1) 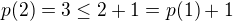
2) Predpokladajme, ze  a chceme dokazat, ze
a chceme dokazat, ze 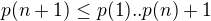 .
.
A potom to dokazes bez vyuzitia toho predpokladu, ale to formalne vobec nevadi.
EDIT: tak ma este napadlo, ze ta indukcia by tam mala zmysel, keby si este akoze ani nemala vetu, ze prvocisel je nekonecne vela a teda ani to, ze z nich mozes vyrobit postupnost. A potom by si chcela dokazat nieco v tomto duchu:
Dokazte, ze existuje postupnost  splnajuca
splnajuca  a prebiehajuca cez vsetky prvocisla.
a prebiehajuca cez vsetky prvocisla.
Potom by sa teda ta indukcia pekne pouzila na zrozumitelnu konstrukciu tej postupnosti.
Offline
#5 23. 09. 2013 14:52 — Editoval Formol (23. 09. 2013 14:55)
Re: Důkaz indukcí
Omlouvám se, ale přivedl jsem tě tak trochu na zcestí, protože se mi na první pohled zdálo, že využiješ toho, že na pravé straně máš prvočíslo.
Nejprve předpoklad: Např. pro n=2 to platí, protože 7<=2*3+1=7
Dále indukční krok. Tady jde použít Cimrmanův krok stranou, protože konstrukce vyššího prvočísla z důkazu nekonečného počtu ti nezaručuje, že jde o nejbližší vyšší prvočíslo. Zaručuje ti ovšem, že jde o horní závoru; tedy když to pro n prvočísel platí, lze analogicky vytvořit horní závoru i pro n+1 prvočísel. Tedy platí-li vztah pro n, platí i pro n+1.
Ono se může zdát, že jde o něco samoúčelného a že v tom indukce není nutná, protože "je to vidět". To je ale omyl, ty chceš ukázat, že to pro všechna n platí, takže musíš postupovat induktivně. Až se později dostaneš ke složitějším konstrukcím, tak zjistíš, že u řady důkazů zajímavých vět je nejprve třeba ukázat, že vůbec existují objekty, o kterých dané tvrzení něco vypovídá - a na to jsou takovéhle "zbytečné komplikace" celkem dobrou přípravou.
EDIT: Omlouvám se za duplicitní odpověď, vytvářel jsem ji v průběhu pracovního procesu, takže jsem přehlédl, že Brano odpověděl dříve a lépe.
Доктор сказал «в морг» — значит в морг!
Offline

 .
. 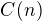 není prvočíslo ,
není prvočíslo , . Z předpokladů o posloupnosti
. Z předpokladů o posloupnosti  a z (1)
a z (1)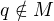 , tedy
, tedy  .
. 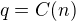 .
.  obsahuje aspoň jedno prvočíslo (konktretně
obsahuje aspoň jedno prvočíslo (konktretně  ).
).  .
.