Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 01. 2009 20:05
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Integrál
Offline
#4 16. 01. 2009 20:12
Re: Integrál
↑ Frantik88:
Tvá cesta je kontraproduktivní volbou. Následoval bych rad ↑ BrozekP:. V podstatě používá lineární substituci t=-x.
Offline
#6 16. 01. 2009 20:24 — Editoval BrozekP (16. 01. 2009 20:26)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Integrál
Ano, snadno si výsledek integrování můžeš ověřit tak, že ho zderivuješ a musí vyjít integrand. To odpovídá tomu, jak je definována primitivní funkce.
Offline
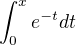 Integrál s mezemi od 0 do x z e na méně t, nevím si s ním rady
Integrál s mezemi od 0 do x z e na méně t, nevím si s ním rady![kopírovat do textarea $\int_0^x\textrm{e}^{-t}\textrm{d}t=-\int_0^x(-1)\textrm{e}^{-t}\textrm{d}t=-[\textrm{e}^{-t}]_0^x$](/mathtex/5c/5c7adcbce4790203066e064579d46b8e.gif)
 ... hm?
... hm?