Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 30. 09. 2013 14:52
Re: 1 na nekonečno?
Ahoj ↑ Freedy:,
Klasicky priklad 
toto ma limitu v  ktora je
ktora je  .
.
A pri tom 
a tiez 
Staci?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 30. 09. 2013 15:08
Re: 1 na nekonečno?
Ale já nepočítám s ničím takovým jako je 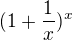
Mě jen zajímá proč součin nekonečnýho množství jedniček, není jednička ale nedefinovanej výraz?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 30. 09. 2013 15:27
Re: 1 na nekonečno?
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 30. 09. 2013 15:36 — Editoval vanok (30. 09. 2013 15:40)
Re: 1 na nekonečno?
Mozes mi upresnit presne o aky vyraz ti ide.
Ak vsak ide o sucin samych 1, takyto sucin ma vzdy hodnotu 1, pre akykolvek pocet jednotiek, tak limita takeho sucinu je tiez 1.
Toto ti mozno bude uzitocne:
http://cs.wikipedia.org/wiki/Nekonečný_součin
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 30. 09. 2013 16:23
Re: 1 na nekonečno?
↑ gadgetka: pěkné video, právě sem ho dokoukal, ale tohle neni přesně to na co se ptám. Vím že tohle platí, ale netuším proč se prostě 1^nekonečno nedefinuje jako 1 ale jako nedefinovano.
Jaká je teda limita:
když to neni definováno?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 30. 09. 2013 17:43 — Editoval Bati (30. 09. 2013 17:47)
Re: 1 na nekonečno?
↑ Freedy:
Limita přece není definována jako obyčejné dosazení. Pokud se bavíme o limitách funkcí, tak takové dosazení funguje jen v případě, že daná funkce je v dosazovaném bodě spojitá. Žádná funkce není spojitá v nekonečnu v běžném smyslu (v  ).
).
V tomto konkrétním případě je ta limita samozřejmě rovna 1, neboť platí  . To proto, že 1 umocněná na jakékoliv reálné číslo je opět 1.
. To proto, že 1 umocněná na jakékoliv reálné číslo je opět 1.
Samozřejmě, že by šlo definovat  , ale bylo by to naprosto k ničemu, jen by pak existovaly 2 symboly pro to samé.
, ale bylo by to naprosto k ničemu, jen by pak existovaly 2 symboly pro to samé.
Offline
#10 30. 09. 2013 18:34 — Editoval Freedy (30. 09. 2013 18:35)
Re: 1 na nekonečno?
Nechtěl sem definovat
ale prostě a logicky: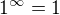
achjo, asi budu muset přehodnotit svůj názor, že matika dává smysl...
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#12 30. 09. 2013 18:56
Re: 1 na nekonečno?
ale znamená to že 1^nekonečno je prostě jedna... když budu jedničku donekonečna násobit jedničkou tak to prostě bude jednička!... Hlavně že nula ve jmenovateli se rovná +- nekonečno ale součin nekonečně mnoho jedniček prostě matika nedefinovala...
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 30. 09. 2013 19:22
Re: 1 na nekonečno?
↑ Freedy:
Tady jde hlavně o to, že když počítáš limitu třeba  , tak výsledek není
, tak výsledek není  . Stejně tak neplatí, že
. Stejně tak neplatí, že 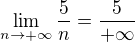 . Tyhle divné výrazy se ve výsledku nesmí objevit, stejně jako tam nesmí zbýt žádné
. Tyhle divné výrazy se ve výsledku nesmí objevit, stejně jako tam nesmí zbýt žádné  . Limity se zpravidla počítají použitím nějakých vět o součtu, součinu apod. Jenže na SŠ se s tím nedá patlat do všech detailů, a tak se to celé ochcává tím, že se řekne něco jako "vyšel výraz typu pět děleno nekonečno", to se napíše jako výsledek té limity (my jsme to na gymplu psali do uvozovek, abychom věděli že jsme na tenkém ledě), a ten limitní přechod se udělá potom selsky.
. Limity se zpravidla počítají použitím nějakých vět o součtu, součinu apod. Jenže na SŠ se s tím nedá patlat do všech detailů, a tak se to celé ochcává tím, že se řekne něco jako "vyšel výraz typu pět děleno nekonečno", to se napíše jako výsledek té limity (my jsme to na gymplu psali do uvozovek, abychom věděli že jsme na tenkém ledě), a ten limitní přechod se udělá potom selsky.
Jenže tohle právě u těch nedefinovaných výrazů pak vypadá blbě, třeba v tom případě  . Svádí to k té otázce jak jednička pořád dokola násobená jedničkou může dát něco jiného než jedničku. A ona nemůže. Jenže to by odpovídalo výpočtu jiné limity, a to sice
. Svádí to k té otázce jak jednička pořád dokola násobená jedničkou může dát něco jiného než jedničku. A ona nemůže. Jenže to by odpovídalo výpočtu jiné limity, a to sice  . V případě té mé první limity (definice e) je to něco jiného, je to výraz "typu"
. V případě té mé první limity (definice e) je to něco jiného, je to výraz "typu"  . To ale znamená, že každý člen je ne nutně jednička, ale něco co jde k jedničce umocněný na něco co jde k nekonečnu. To už k jedničce konvergovat nemusí.
. To ale znamená, že každý člen je ne nutně jednička, ale něco co jde k jedničce umocněný na něco co jde k nekonečnu. To už k jedničce konvergovat nemusí.
Offline
#15 30. 09. 2013 22:38
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: 1 na nekonečno?
↑ Freedy:
======
Mě jen zajímá proč součin nekonečnýho množství jedniček, není jednička ale nedefinovanej výraz?
======
Součin nekonečného počtu jedniček je jednička, a to ze stejného důvodu, proč součet nekonečného počtu nul je nula.
Budoucnost patří aluminiu.
Offline
#16 30. 09. 2013 22:52
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: 1 na nekonečno?
↑ kryštof:
To bys řekl hodně špatně. Součiny nekonečně mnoha činitelů jsou definovány prakticky stejně jako součty nekonečně mnoha sčítanců a platí např.
Budoucnost patří aluminiu.
Offline
#17 30. 09. 2013 22:58
Re: 1 na nekonečno?
Hm, myslím že to, že stále nemůžu najít jednoznačnou větu, která by dokazovala důvod proč je 1 ^ nekonečno nedefinovano, znamená, že to prostě není logicky, proto to ani nejde vysvětlit.
Prostě pokud se s tím v nějakym testu setkám, suveréně to budu psát jako 1 a ne jako nedefinovanej výraz. A moc rád bych viděl toho kdo by mi to opravoval, co by mi řek za argument.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#18 30. 09. 2013 23:01 — Editoval Creatives (30. 09. 2013 23:04) Příspěvek uživatele Creatives byl skryt uživatelem Creatives.
#19 30. 09. 2013 23:17
Re: 1 na nekonečno?
"Hm, myslím že to, že stále nemůžu najít jednoznačnou větu, která by dokazovala důvod proč je 1 ^ nekonečno nedefinovano, znamená, že to prostě není logicky, proto to ani nejde vysvětlit."
No tak daj argument, prečo by sa 1 na nekonečno definovať malo :D
1^6 - 2^6 + 3^6 = 666
Offline
#21 30. 09. 2013 23:29
Re: 1 na nekonečno?
↑ Freedy:
Jo jo, a vůbec nejlepší bude udělat to v testu z limit, třeba právě pro výpočet té co se tu párkrát objevila  . Tam to ušetří hodně práce. Ale nakonec proč si pamatovat nějakou pitomou definici Eulerova čísla, když si můžu sám definovat něco co se mi líbí a počítat to jinak. Sice mi vyjde jiný výsledek než ostatním, ale holt ostatní nejsou neomylní, a nemohou mít všechno správně. Já jim to odpustím. Opravdu je tohle přístup který tě posune dál?
. Tam to ušetří hodně práce. Ale nakonec proč si pamatovat nějakou pitomou definici Eulerova čísla, když si můžu sám definovat něco co se mi líbí a počítat to jinak. Sice mi vyjde jiný výsledek než ostatním, ale holt ostatní nejsou neomylní, a nemohou mít všechno správně. Já jim to odpustím. Opravdu je tohle přístup který tě posune dál?
Plácáš tu blbosti, například tohle "Hlavně že nula ve jmenovateli se rovná +- nekonečno" taky není pravda. Někde na základce bylo jasně řečeno, že nulou dělit nelze, a nic se od té doby nezměnilo. Je to jen jakési zhuštěné vyjádření věty o limitě podílu, kterou neznáš. Nekonečno není normální číslo, když se s ním pracuje tak je za tím zpravidla schovaná nějaká limita, a s ohledem na to se pak chováme k těm podivnostem jako 0/nekonečno atd.
Jsem zvědavý, jak odpovíš na Hanisovu otázku.
Offline
#23 01. 10. 2013 00:00
Re: 1 na nekonečno?
↑ Freedy:
Ano, to je správně. A uvědom si kde přesně je ten problém. 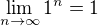 , přesně jak jsi čekal, to ano. Ale to co Hanis píše do těch hranatých závorek, tam už se část té informace ztratila. On tam totiž píše jen limity toho základu a exponentu. V té posloupnosti základů ale nejsou (nemusí být) všechny členy jedničky - jsou tam čísla, která se postupně k jedničce blíží, a to není to samé.
, přesně jak jsi čekal, to ano. Ale to co Hanis píše do těch hranatých závorek, tam už se část té informace ztratila. On tam totiž píše jen limity toho základu a exponentu. V té posloupnosti základů ale nejsou (nemusí být) všechny členy jedničky - jsou tam čísla, která se postupně k jedničce blíží, a to není to samé.
Ono je to podobné jako výraz  . Např.
. Např.  , ale
, ale  , přestože obě jsou "nekonečno děleno nekonečnem". Tady je to vidět líp. kde je problém. Když si vypíšu zvlášť ty limity čitatele a jmenovatele, tak ztratím informaci o tom která posloupnost se k tomu nekonečnu blíží "rychleji", a to je pro výsledek podstatné.
, přestože obě jsou "nekonečno děleno nekonečnem". Tady je to vidět líp. kde je problém. Když si vypíšu zvlášť ty limity čitatele a jmenovatele, tak ztratím informaci o tom která posloupnost se k tomu nekonečnu blíží "rychleji", a to je pro výsledek podstatné.
Offline
#24 01. 10. 2013 00:05
Re: 1 na nekonečno?
Je mi to už jasné dostatečně... :-/ Asi jen předbíhám, počkám si na dokonalé vysvětlení limit někde na vysoké škole, jelikož na střední se toho asi těžko dočkám... :-//
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#25 01. 10. 2013 09:53 — Editoval Rumburak (01. 10. 2013 09:57)
Re: 1 na nekonečno?
↑ Freedy:
Ahoj.
Pokud symbol 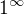 chápeme pouze jako mnemotechnické označení limit funkcí tvaru např.
chápeme pouze jako mnemotechnické označení limit funkcí tvaru např.  ,
,
když  , tak rozumným způsobem (aby vhovoval všem takovým případům)
, tak rozumným způsobem (aby vhovoval všem takovým případům)
být definován nemůže, o čem Tě, zdá se, předložené příklady už přesvědčily.
ALE:
Chápeme-li zde číslo  jako KOSNSTANTU
jako KOSNSTANTU  (neboli je-li výše uvažovaná funkce
(neboli je-li výše uvažovaná funkce  identicky rovna
identicky rovna  ) ,
) ,
pak s definicí  by nebyl problém. Skutečně totiž platí např.
by nebyl problém. Skutečně totiž platí např.
 ,
,
pojednává o tom partie o nekonečných součinech, zkus prohledat www.
Rovněž  .
.
Offline


 a
a 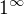 je zásadní rozdíl a to ten, že to první je normálně definováno.
je zásadní rozdíl a to ten, že to první je normálně definováno.![kopírovat do textarea $ \lim_{n \to \infty}\(e^{\frac{1}{n}}\)^n=[1^{\infty}]=$](/mathtex/1e/1ea26e3c3a7089d9afc286b2ef0d0c03.gif)
![kopírovat do textarea $ \lim_{n \to \infty}\(e^{\frac{-1}{n}}\)^{n^2}=[1^{\infty}]=$](/mathtex/b2/b2716ac8371ca7c4b098cd1cce0788b5.gif)
![kopírovat do textarea $ \lim_{n \to \infty}\(e^{\frac{1}{n}}\)^{n^2}=[1^{\infty}]=$](/mathtex/73/73661caf0ebcd8bdd8003215a36603fd.gif)
![kopírovat do textarea $ \lim_{n \to \infty}\(e^{\frac{(-1)^n}{n}}\)^{n}=[1^{\infty}]=$](/mathtex/d7/d79ebea3d0ab514c27ce2d2c8e387621.gif)



 --- nemá řešení...
--- nemá řešení...