Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Supremum fce arctg (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 10. 2013 12:52
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Supremum fce arctg
Zdravím,
Nevím si rady s tímto příkladem  Mohl by mi nekdo napsat postup? Diky
Mohl by mi nekdo napsat postup? Diky
Offline
- (téma jako vyřešené označil(a) OndraVesely)
#2 10. 10. 2013 13:42 — Editoval Brano (10. 10. 2013 13:45)
Re: Supremum fce arctg
najprv treba vysetrit vnuotrnu fciu t.j.
kde  je parameter.
je parameter.
Ak 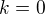 tak je to trivialne
tak je to trivialne  (len v
(len v  nie je definovana, tak ju tam mozme takto dodefinovat). Ak nie, tak zavedme substituciu
nie je definovana, tak ju tam mozme takto dodefinovat). Ak nie, tak zavedme substituciu  - ta je bijektivna na
- ta je bijektivna na 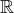 tak nestracame ziadnu informaciu a dostaneme
tak nestracame ziadnu informaciu a dostaneme
a teda mozme skumat iba
to necham na teba - ja som to urobil vo W|A
http://www.wolframalpha.com/input/?i=y% … 283%2F2%29
jedna sa o neparnu fciu - treba najst kde je to maximum
http://www.wolframalpha.com/input/?i=ma … 283%2F2%29
minimum bude teda v 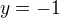
 a
a  dostaneme iba prenasobenim tou konstantou zavisiacou od
dostaneme iba prenasobenim tou konstantou zavisiacou od  a kedze
a kedze  je vsade rastuci, tak max a min toho vyrazu (bez absolutnej hodnoty) bude iba
je vsade rastuci, tak max a min toho vyrazu (bez absolutnej hodnoty) bude iba  vysledkov a ked nakoniec uvazime aj to, ze
vysledkov a ked nakoniec uvazime aj to, ze  je neparny tak ta absolutna hodnota nam da, ze max sa nadobuda aj v
je neparny tak ta absolutna hodnota nam da, ze max sa nadobuda aj v 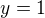 aj v
aj v 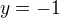 teda
teda
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Supremum fce arctg (TOTO TÉMA JE VYŘEŠENÉ)