Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dotaz k definici lineární závislosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 10. 2013 13:11 — Editoval Akcope (11. 10. 2013 13:15)
Dotaz k definici lineární závislosti
Zdravím, mám krátký dotaz k formální definici LZ a LN;
Řekněme, že mám dva vektory :  . Ty jsou jasně lineárně nezávislé a generují
. Ty jsou jasně lineárně nezávislé a generují  .
.
Nyní do tohoto souboru přidám ještě jeden vektor, který se bude rovnat vektoru x, tento soubor bude následně vypadat takto: 
Tento soubor je prý už lineárně závislý. Nerozumím proč. V souřadnici y sice dokážu dostat nulu netriviální lineární kombinací vektorů z a x, ale na to, abych v souřadnici x dostal 0, tak jediný způsob jak toho dosáhnout, je vynásobit vektor y nulou (není právě definicí nezávislosti to, že soubor je LN právě tehdy, když pouze jeho triviální LK je rovna nulovému vektoru??).
Nebo to je tak, že v definici LN je to myšleno že "musím úplně všechny vektory muset vynásobit nulou, abych dostal nulový vektor"?
Offline
- (téma jako vyřešené označil(a) Akcope)
#3 11. 10. 2013 13:44
- Eratosthenes
- Příspěvky: 2937
- Reputace: 139
Re: Dotaz k definici lineární závislosti
↑ Akcope:
================
v definici LN je to myšleno že "musím úplně všechny vektory muset vynásobit nulou, abych dostal nulový vektor"?
================
Ano, je to přesně tak.
Budoucnost patří aluminiu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dotaz k definici lineární závislosti (TOTO TÉMA JE VYŘEŠENÉ)

 a trojica
a trojica  nie je to iste ako
nie je to iste ako 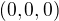 cize je netrivialna.
cize je netrivialna.