Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita postupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#3 17. 10. 2013 19:09
Re: Limita postupnosti
Ahoj,
druhá možnost:![kopírovat do textarea $\sqrt[n]{n!}=e^{\ln(n!)^{\frac1n}}=e^{\frac{\sum_{k=2}^n\ln k}{n}}$](/mathtex/b5/b5465ae9e20f46887abfa47269f8f053.gif) , což by vedlo na Stolzovu větu.
, což by vedlo na Stolzovu větu.
třetí je použít přímo Cauchyho vzorec:![kopírovat do textarea $\lim_{n\to \infty } \sqrt[n]{n!} = \lim_{n\to \infty }\frac{(n+1)!}{n!}$](/mathtex/33/3335255f8b59a6b51057747ea157561f.gif) .
.
Ale rada, od kolegyně ↑ Andrejka3: je elementárnější, takže jsem ty další přidal jen pro zajímavost.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita postupnosti (TOTO TÉMA JE VYŘEŠENÉ)
![kopírovat do textarea $\lim_{n\to \infty } \sqrt[n]{n!} =\infty ? $](/mathtex/d9/d982b847074d128174c31551a0c33cdd.gif) vdaka
vdaka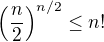 ?
?