Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 10. 2013 03:35
Re: Úplný metrický priestor
↑ klaudia:
Asi by bolo dobre zadefinovať tieto pojmy. Možno sa mýlim, ale myslím, že sa aspoň v niektorých kontextoch používajú ako synonymá.
Napríklad na Wikipedii sa píše:
Precompact set may refer to:
* Relatively compact subspace, a subset whose closure is compact
*Totally bounded set, a subset that can be covered by finitely many subsets of fixed size
http://en.wikipedia.org/wiki/Precompact_set
Offline
#4 20. 10. 2013 10:52
Re: Úplný metrický priestor
klaudia napsal(a):
↑ kompik:
To som našla tiež, ale ako to dokážem matematicky, nemôžem sa odvolať nato, že sú to synonymá...
Nejaké matematické odvodenie nato neexistuje?
Aby malo zmysel hovoriť o matematickom odvodení, treba najprv vedieť definície pojmov, s ktorými pracujeme.
Takže by pomohlo pozrieť sa do poznámok alebo skrípt, podľa ktorých idete a povedať nám ostatným, čo chápete pod prekompaktnou a relatívne kompaktnou množinou.
Offline
#5 20. 10. 2013 11:04
Re: Úplný metrický priestor
Ak je cieľom ukázať to že v úplnom metrickom piestore platí:
Podmnožina A je totálne ohraničená <=> A má kompaktný uzáver,
tak by som si skúsil pomôcť tým, že vieme:
* Metrický priestor je kompaktný práve vtedy, keď je úplný a totálne ohraničený.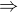 Tu by som skúsil ukázať, že ak A je totálne ohraničená množina, tak aj
Tu by som skúsil ukázať, že ak A je totálne ohraničená množina, tak aj  je totálne ohraničená množina. Potom
je totálne ohraničená množina. Potom  je úplný priestor (lebo je uzavretý podpriestor úplného priestoru). Súčasne je totálne ohraničený. Teda je to kompaktný podpriestor.
je úplný priestor (lebo je uzavretý podpriestor úplného priestoru). Súčasne je totálne ohraničený. Teda je to kompaktný podpriestor.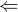 Keďže
Keďže  je kompaktný priestor, tak je aj totálne ohraničený. Stačí zdôvodniť, že podmnožina totálne ohraničenej množiny je totálne ohraničená.
je kompaktný priestor, tak je aj totálne ohraničený. Stačí zdôvodniť, že podmnožina totálne ohraničenej množiny je totálne ohraničená.
Offline
#6 20. 10. 2013 11:34
Re: Úplný metrický priestor
↑ kompik:
Cieľom bolo dokázať, že RELATÍVNE KOMPAKTNÁ MNOŽINA  PREKOMPAKTÁ (TOTÁLNE OHRANIČENÁ) MNOŽINA
PREKOMPAKTÁ (TOTÁLNE OHRANIČENÁ) MNOŽINA
Def. Hovoríme, že M je RELATÍVNE KOMPAKTNÁ MNOŽINA, ak 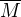 je kompaktná množina (tj. z každej postupnosti prvkov množiny M je možné vybrať konvergentnú postupnosť).
je kompaktná množina (tj. z každej postupnosti prvkov množiny M je možné vybrať konvergentnú postupnosť).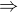 Každá konvergentná postupnosť je cauchyovská postupnosť.
Každá konvergentná postupnosť je cauchyovská postupnosť.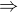 Ak z každej postupnosti prvkov množiny M možno vybrať cauchyovskú postupnosť, potom M je TOTÁLNE OHRANIČENÁ MNOŽINA.
Ak z každej postupnosti prvkov množiny M možno vybrať cauchyovskú postupnosť, potom M je TOTÁLNE OHRANIČENÁ MNOŽINA.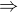 TOTÁLNE OHRANIČENÁ
TOTÁLNE OHRANIČENÁ  PREKOMPAKTÁ
PREKOMPAKTÁ
Teda: RELATÍVNE KOMPAKTNÁ MNOŽINA  PREKOMPAKTÁ
PREKOMPAKTÁ
Mohlo by to byť takto?
Offline
#7 20. 10. 2013 12:50
Re: Úplný metrický priestor
↑ klaudia:
Z toho, čo si napísala, sa dá domyslieť, že vaša definícia totálne ohraničenej množiny je: Z každej postupnosti sa dá vybrať cauchyovská podpostupnosť.
Dôkaz implikácie 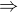 vyzerá byť ok: Z postupnosti vyberieme konvergentnú podpostupnosť. (Táto podpostupnosť konverguje v
vyzerá byť ok: Z postupnosti vyberieme konvergentnú podpostupnosť. (Táto podpostupnosť konverguje v  , limita nemusí byť prvok množiny M. Ale to nemení nič na tom, že postupnosť bude cauchyovská - táto vlastnosť nezávisí od toho, či sa na postupnosť pozeráme v M alebo v uzávere.)
, limita nemusí byť prvok množiny M. Ale to nemení nič na tom, že postupnosť bude cauchyovská - táto vlastnosť nezávisí od toho, či sa na postupnosť pozeráme v M alebo v uzávere.)
Ešte by bolo treba nejako zdôvodniť opačnú implikáciu 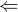 . T.j. ak množina M je totálne ohraničená, tak jej uzáver
. T.j. ak množina M je totálne ohraničená, tak jej uzáver  je kompaktná množina.
je kompaktná množina.
Ak by som to robil cez postupnosti, tak prvá možnosť, ktorá mi prišla na um je takáto:
* Máme ľubovoľnú postupnosť  v
v  .
.
* Zoberieme si postupnosť prvok z M takú, že  . (To sa dá - stačí si spomenúť na definíciu uzáveru.)
. (To sa dá - stačí si spomenúť na definíciu uzáveru.)
* Z nej sa dá vybrať cauchyovská podpostupnosť  .
.
* Potom aj  je cauchyovská. Keďže
je cauchyovská. Keďže  je úplný priestor, bude táto postupnosť aj konvergentná.
je úplný priestor, bude táto postupnosť aj konvergentná.
Offline

