Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 10. 2013 19:53
posloupnosti
Ahoj,
prosím o pomoc s následujícím příkladem, absolutně si nevím rady:
Nechť posloupnosti  kde
kde 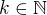 jsou neomezené. Musí existovat posloupnost
jsou neomezené. Musí existovat posloupnost  taková, že
taková, že  ;
; 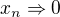 a všechny:
a všechny:
a) 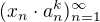 konvergují?
konvergují?
b) 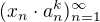 divergují?
divergují?
Prosím o podrobnější návod, bojím se, že lehké "pošťouchnutí" mi nepomůže :)
Díky
Offline
#5 23. 10. 2013 11:37
Re: posloupnosti
↑ rama27: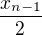 je tam proto, abych tu posloupnost pak mohl odhadnout shora konvergentní posloupností
je tam proto, abych tu posloupnost pak mohl odhadnout shora konvergentní posloupností  . Ale teď si uvědomuju, že to tam je asi zbytečné - divergence všech posloupností
. Ale teď si uvědomuju, že to tam je asi zbytečné - divergence všech posloupností 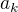 zaručuje konvergenci
zaručuje konvergenci 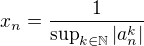 k nule.
k nule.
Absolutní hodnota je tam proto, že dělám supremum - to by pak nemělo moc smysl, kdyby tam byl nějaký obrovský záporný člen.
Offline
#9 23. 10. 2013 23:13
Re: posloupnosti
↑ rama27:
Ta je tam, abych zaručil divergenci té součinové posloupnosti. Kdyby tam nebyla, mohl bych teoreticky dostat konstantní posloupnost, která nediverguje. Přesněji: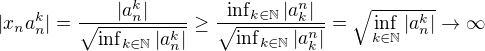 .
.
Klidně se ptej, tenhle příklad vidím poprvé a přijde mi docela zajímavý.
Offline
#10 23. 10. 2013 23:51 — Editoval user (24. 10. 2013 00:05)
Re: posloupnosti
Ahoj,
omlouvám se, že vstupuji do rozpracovaného tématu. Ale ze zadání mi není zcela jasné, jestli je  přirozené, ale pevně zvolené.
přirozené, ale pevně zvolené.
Nejsem si jistý, jak je potom zajištěno, že 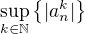 je konečné číslo.
je konečné číslo.
U druhého příkladu by podle mne mělo být určitě vybíráno minimálně 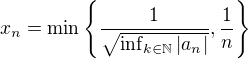 , protože ze zadání neomezenosti posloupností neplyne, že by nemohlo být nekonečně mnoho členů omezených (rovných 1, aby to v našem případě mocnění nezměnilo), čímž bychom neměli zajištěnou konvergenci
, protože ze zadání neomezenosti posloupností neplyne, že by nemohlo být nekonečně mnoho členů omezených (rovných 1, aby to v našem případě mocnění nezměnilo), čímž bychom neměli zajištěnou konvergenci  .
.
Offline
#11 24. 10. 2013 00:18 — Editoval user (24. 10. 2013 00:20)
Re: posloupnosti
Myslím si, že první případ by šel vyřešit nakonec snad jinak protože členy původní  , rostou v
, rostou v  polynomiálně, tudíž by je možná bylo možné přebít posloupností, která by rostla exponenciálně, něco jako
polynomiálně, tudíž by je možná bylo možné přebít posloupností, která by rostla exponenciálně, něco jako 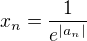 , ale nejsem si tím moc jistý a nemám to úplně promyšlené, takže je možné, že to je blbost. Protože by se v důkaze muselo operovat i s
, ale nejsem si tím moc jistý a nemám to úplně promyšlené, takže je možné, že to je blbost. Protože by se v důkaze muselo operovat i s  , ale možná by šlo ukázat, že pro každé
, ale možná by šlo ukázat, že pro každé  od jistého
od jistého 
 převáží.
převáží.
Offline
#12 24. 10. 2013 09:36
Re: posloupnosti
Offline
#13 24. 10. 2013 20:59 — Editoval user (24. 10. 2013 21:04)
Re: posloupnosti
Prozatím budu uvažovat jen o posloupnostech ze zadání s touto vlastností 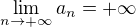 .
.
Využívám toho, že platí
Označím 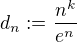 . Dále používám limitu
. Dále používám limitu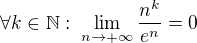 .
.
Pak není těžké ukázat pro posloupnost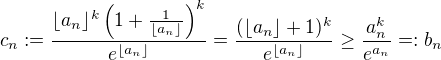 ,
,
že je má stejnou limitu jako 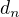 (je to součin skorovybrané posloupnosti z
(je to součin skorovybrané posloupnosti z 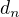 a posloupnosti s limitou 1) , takže má stejnou limitu a zároveň mi poskytuje horní odhad pro
a posloupnosti s limitou 1) , takže má stejnou limitu a zároveň mi poskytuje horní odhad pro 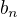 .
.
To by podle mě mohlo stačit.
V úvahách jsem použil faktů, že 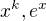 jsou monotonní funkce a že
jsou monotonní funkce a že  .
.
Snad jsem se nikde neseknul.
Offline
#15 25. 10. 2013 00:29
Re: posloupnosti
To zase nenapadlo mě. Podle té věty, že jsou ty posloupnosti neomezené by to tak mohlo být, protože jinak by stačilo zadat neomezenost  ...
...
Každopádně bych počkal na vyjádření autora. Ale doufám, že ať to je jakkoliv, tak příspěvky budou alespoň trošku přínosné.
Offline

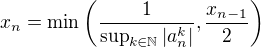 .
.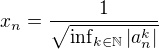 .
.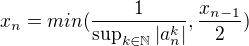
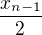
 si dal do absolutní hodnoty proto, že chceš, aby všechny členy posloupnosti byly kladné?
si dal do absolutní hodnoty proto, že chceš, aby všechny členy posloupnosti byly kladné?