Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 10. 2013 19:05
Graf závislosti teploty na čase
Ahoj, mám za úkol sestrojit graf závislosti teploty na čase.
Mám zadanou hmotnost látky, počáteční teplotu, konečnou teplotu a výkon zařízení, ve kterém se látka ohřívá.
Jak mám sestrojit graf závislosti teploty na čase?
Děkuji.
Offline
- (téma jako vyřešené označil(a) Olínečka)
#4 27. 10. 2013 13:26
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Graf závislosti teploty na čase
OK, v tom prípade máš všetko čo potrebuješ na zostrojenie grafu.
Uvažujem len priamu bezstratovú výmenu tepla medzi ohrievačom a vodou, keďže nespomínaš nič také ako tepelné straty, účinnosť ohrievača ani príspevok tepelnej kapacity nádoby, v ktorej je voda.
Teplo  , vyprodukované ohrievačom s výkonom
, vyprodukované ohrievačom s výkonom  za čas
za čas 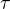 je rovné
je rovné 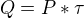
Toto teplo bude absorbované vodou o hmotnosti  , s tepelnou kapacitou
, s tepelnou kapacitou  a počiatočnou teplotou
a počiatočnou teplotou 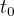 , pričom sa zohreje na konečnú teplotu
, pričom sa zohreje na konečnú teplotu  podľa vzťahu
podľa vzťahu 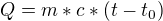
Z oboch rovníc ľahko určíš čas 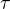 , za ktorý sa voda ohreje na teplotu
, za ktorý sa voda ohreje na teplotu  . Graf potom vyzerá ako priamka, na jej určenie stačia dva body. Prvý bod máš, to je počiatočná teplota v čase t = 0, druhý bod je tvoja konečná teplota
. Graf potom vyzerá ako priamka, na jej určenie stačia dva body. Prvý bod máš, to je počiatočná teplota v čase t = 0, druhý bod je tvoja konečná teplota  a čas
a čas 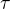 . Ak potrebuješ mať viac bodov v grafe, môžeš si pomocou horeuvedených vzťahov dopočítať, aká bude teplota vody za rôzny čas.
. Ak potrebuješ mať viac bodov v grafe, môžeš si pomocou horeuvedených vzťahov dopočítať, aká bude teplota vody za rôzny čas.
Offline
#6 27. 10. 2013 17:49 — Editoval Olínečka (27. 10. 2013 17:58)
Re: Graf závislosti teploty na čase
Ještě mám dotaz na podobný příklad:
(Vím, že každý příklad má být v jednom tématu, ale když je to skoro stejný příklad, přijde mi to zbytečné)
Mám opět sestrojit graf závislosti teploty na čase. Mám zadáno: P, m1, m2, c, t0 - počáteční teplota, t1, tv - výsledná teplota. Nejdřív se do přístroje dá látka o hmotnosti m1 a teplotě t0, po dosažení teploty t1 se přidá stejná látka o hmotnosti m2 a teplotě t0 a má se to ohřát na teplotu tv.
Jak bude vypadat graf závislosti na čase?
Nešel by ten čas, za který se látka ohřeje na výslednou teplotu, vypočítat nějak takhle?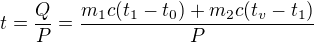
A jak bude vypadat ten graf?
Díky.
Offline
#7 27. 10. 2013 18:20 — Editoval KennyMcCormick (27. 10. 2013 18:26)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Graf závislosti teploty na čase
Jak bude vypadat graf závislosti na čase?
Dotýkají se ty látky spolu navzájem?
Nešel by ten čas, za který se látka ohřeje na výslednou teplotu, vypočítat nějak takhle?
Jestli ty látky nejsou v kontaktu, tak ten čas je obecně různý, a musíš obě látky počítat zvlášť.
Jestli v kontaktu jsou, tak ohříváš první látku z teploty 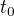 na teplotu
na teplotu 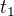 , a potom z teploty
, a potom z teploty 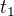 na teplotu
na teplotu 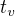 . Druhou látku ohříváš z teploty
. Druhou látku ohříváš z teploty 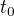 na teplotu
na teplotu 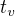 . Takže to bude:
. Takže to bude: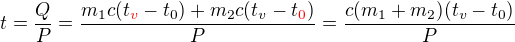 .
.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#9 27. 10. 2013 19:35 — Editoval Olínečka (27. 10. 2013 19:40)
Re: Graf závislosti teploty na čase
Už tenhle příklad asi chápu, díky.
Ještě tu mám příklad:
Nejdřív se do přístroje dá látka o hmotnosti m a teplotě t0, ohřeje se na teplotu t1 a odleje se od toho část látky o hmotnosti m1 a teplotě t1 a pak se látka o hmotnosti m-m1 ohřeje z teploty t1 na teplotu tv. Jak tady u toho vypočítám čas?
Nemohlo by to být: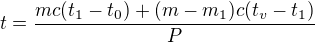
?
Offline
