Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Magnetické pole (indukcia) valcovej cievky v ľubovoľnom bode priestoru (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 10. 2013 14:54
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Magnetické pole (indukcia) valcovej cievky v ľubovoľnom bode priestoru
Po dlhej dobe zdravím!
Mám menší problém s jedným zadaním. Ide o výpočet magnetickej indukcie valcovej cievky v ľubovoľnom bode priestoru. Na radu môjho školiteľa by som to mal vedieť počítať integrovaním priamo podľa Biot-Savartovho zákona, no pri hľadani jednoduchšieho prípadu, a síce výpočtu magn. indukcie prúdovej slučky (vychádzal som zo str. 262-263 týchto skrípt a z tohto materiálu), mi príde oveľa výhodnejšie spočítať vektorový potenciál a jeho rotáciou potom vypočítať indukciu.
Skúsil som teda prípad prúdovej slučky rozšíriť na valcovú cievku. Stred cievky som stotožnil s počiatkom sústavy a jej os s osou  . Cievka je zobrazená ako plocha valca s polomerom
. Cievka je zobrazená ako plocha valca s polomerom  a dĺžkou
a dĺžkou 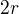 , čiarkovane je naznačený rez cez valcovú plochu rovinou
, čiarkovane je naznačený rez cez valcovú plochu rovinou 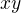 . Bod
. Bod  je bod v ktorom chcem vypočítať vektorový potenciál
je bod v ktorom chcem vypočítať vektorový potenciál  . Jeho vzdialenosť od elementu je
. Jeho vzdialenosť od elementu je  , pomocou polárneho uhla
, pomocou polárneho uhla  a azimutálneho uhla
a azimutálneho uhla  viem určiť vzdialenosť
viem určiť vzdialenosť  ako
ako
Pre prúdovú slučku je vektorový potenciál daný uzavretým krivkovým integrálom ,
,
kde  je dĺžkový ekement krivky
je dĺžkový ekement krivky  ,
,  je permeabilita,
je permeabilita,  je veľkosť prúdu prech. slučkou,
je veľkosť prúdu prech. slučkou,  je vzdialenosť elementu
je vzdialenosť elementu  od bodu, v ktorom vektorový potenciál počítam (značenie podľa skrípt vyššie). Moja valcová cievka je ale plocha, teda po započítaní azimutálneho uhla
od bodu, v ktorom vektorový potenciál počítam (značenie podľa skrípt vyššie). Moja valcová cievka je ale plocha, teda po započítaní azimutálneho uhla  mi integrál prejde na plošný. Problem, s ktorým si neviem rady je, ako previesť tento uzavretý krivkový integrál na plošný, keďže mnou uvažovaná plocha nie je konturovaná krivkou
mi integrál prejde na plošný. Problem, s ktorým si neviem rady je, ako previesť tento uzavretý krivkový integrál na plošný, keďže mnou uvažovaná plocha nie je konturovaná krivkou  a teda nemôžem použiť Stokesovu vetu. Viete niekto poradiť, ako tento problém vyriešiť?
a teda nemôžem použiť Stokesovu vetu. Viete niekto poradiť, ako tento problém vyriešiť?
Náčrt celej úlohy:
Offline
- (téma jako vyřešené označil(a) jelena)
#2 28. 10. 2013 09:10
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Magnetické pole (indukcia) valcovej cievky v ľubovoľnom bode priestoru
Pardon, našiel som v zadaní chybu, vzdialenosť  má byť vyjadrená ako
má byť vyjadrená ako
Dúfam, že mi niekto poradí, už si s tým lámem hlavu niekoľko dní, ale zatiaľ som na nič neprišiel.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Magnetické pole (indukcia) valcovej cievky v ľubovoľnom bode priestoru (TOTO TÉMA JE VYŘEŠENÉ)