Matematické Fórum

Grimmat · 29. 10. 2013 16:48

Zdravím, potřeboval bych poradit s jedním problémem v Maximě. Jde o funkci, která vypíše aritmetický průměr z celých čísel ležících v zadaném intervalu a musí to platit i pro případ, kdy b bude menší než a. Nevím si rady ani s tím jak bych na toto měl napsat vývojový diagram.

mák · 29. 10. 2013 18:12

Zdravím,
aritmetický průměr z řady všech celých čísel ležícím v daném intervalu $a$ až $b$ je:
$\frac{a+b}{2}$
platí to samozřejmě i pro $b<a$ .

svobis · 30. 10. 2013 18:51

ono to má být v intervalu jak čtu. takže tímto co je nademnou spočítám aritmetický průměr pouze koncových bodů a b ale ne aritmetický průměr celých čísel v intervalu <a,b>. v tom je z mého pohledu největší záludnost. a zde už neporadím

kaja.marik · 30. 10. 2013 19:26

Zas tak velka zaludnost to neni. Podle me na to staci nejmensi a nejvetsi cele cislo z toho intervalu a vzorecek pro soucet aritmeticke rady.

mák · 30. 10. 2013 19:31

Aritmetický průměr se spočítá tak, že se součet všech čísel vydělí počtem čísel.
Součet čísel v intervalu $a$ až $b$ je:
$\sum_{i=a}^{b}{i}={{\left(b-a+1\right)\,\left(b+a\right)}\over{2}}$
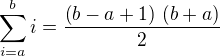
počet čísel v tom samém intervalu je:
$b-a+1$
A pokud to vydělím vyjde:
${{\sum_{i=a}^{b}{i}}\over{b-a+1}}={{{{\left(b-a+1\right)\,\left(b+a\right)}\over{2}}}\over{b-a+1}}={{b+a}\over{2}}$
Připouštím, že je tu jistá podobnost s aritmetickým průměrem čísla $a$ a $b$ .

Matematické Fórum

#1 29. 10. 2013 16:48

Funkce v Maximě

#2 29. 10. 2013 18:12

Re: Funkce v Maximě

#3 30. 10. 2013 18:51

Re: Funkce v Maximě

#4 30. 10. 2013 19:26

Re: Funkce v Maximě

#5 30. 10. 2013 19:31

Re: Funkce v Maximě

Zápatí