Matematické Fórum

Akcope · 30. 10. 2013 23:26

Zdravím, potřeboval bych objasnit tuto větu:

Nechť V je vektorový prostor nad tělesem T. Nechť $P\subset \subset V,Q\subset \subset V, dim(P)<\infty ,dim(Q)<\infty$ . Potom platí:

$dim(P+Q)+dim(P\cap Q) = dim(P)+dim(Q)$

Proč je to takto formulované? Z čeho to plyne?

Já si to představoval asi takhle:

$dim(P+Q) = max\{dim(P),dim(Q)\}$

$dim(P\cap Q) \le max\{dim(P),dim(Q)\}$

Je tato úvaha špatná? A pokud ano, proč?

Předem díky za odpověď.

Andrejka3 · 31. 10. 2013 00:40

↑ Akcope:
Ahoj.
$dim(P+Q) = max\{dim(P),dim(Q)\}$ je špatně. Představ si geometricky: Rovina s počátkem je prostor a v něm jsou dva podprostory - dvě přímky procházející počátkem. Pokud nesplývají, pak jejich spojení je celým prostorem (rovinou).

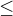$dim(P\cap Q) \le max\{dim(P),dim(Q)\}$ To je pravda. $\dim$ je monotónní vzhledem k inkluzi a a $P\cap Q \leq P$ a $P\cap Q \leq Q$ , kde $\leq$ značí být podprostorem ( $\subset\subset$ akorát se to líp píše).

Ta věta se dokazuje tak, že vezmeš basi průniku a doplníš na basi P, resp. Q. Ověříš, že base průniku a všechny vektory co jsi doplnoval tvoří basi celého prostoru.

Matematické Fórum

#1 30. 10. 2013 23:26

První věta o dimenzi

#2 31. 10. 2013 00:40

Re: První věta o dimenzi

Zápatí