Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 01. 2009 21:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita
Ahoj, snad tě můj příspěvek nebude iritovat, považuji se spíš za teoretika :-)
1 je správně.
Offline
#4 19. 01. 2009 21:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita
↑ ttopi:
Myslím, že 1/x je v exponentu.
Offline
#5 19. 01. 2009 21:48
Re: Limita
no tak graf ma vyjit takhle http://wood.mendelu.cz/math/maw/graf/gr … ko=Odeslat.
Ja jsem si to upravil na e na lim f(x) a pak L'hopitaloval az na lim 1/x..
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#7 19. 01. 2009 21:53 — Editoval BrozekP (19. 01. 2009 21:55)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita
Myslím, že to má být 
↑ gekoncik:
Ten postup převedení na exponencielu je dobře, dál si nejsem jistý, po l'Hospitalovi mi vyšlo něco jiného.
Offline
#8 19. 01. 2009 21:57 — Editoval BrozekP (19. 01. 2009 21:57)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita


Offline
#9 19. 01. 2009 22:00 — Editoval gekoncik (19. 01. 2009 22:05)
Re: Limita
BrozekP napsal(a):
Ale preci v tom zlomku ti vyjde oo . oo tak to pak musis jeste upravit ne?
[img=http://img90.imageshack.us/img90/2015/dsc00102gp7.th.jpg]
Omlouvam se za kvalitu ale nemel jsem k dispozici fotak..
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#10 19. 01. 2009 22:03
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita
↑ gekoncik:
Když máš něco, co ti jde do nekonečna, a vynásobíš to něčím jiným, co jde také do nekonečna, tak součin jde přeci do nekonečna. Když to bude ve jmenovateli, tak zlomek půjde do nuly.
Problém je, když se nekonečno dělí nekonečnem, od nekonečna odčítá nekonečno...
Offline
#11 19. 01. 2009 22:07
Re: Limita
Aha vlastne to je soucin nekonecen takze je to nekonecno :) To me nenapadalo :)
Problém je, když se nekonečno dělí nekonečnem, od nekonečna odčítá nekonečno...?? Takze rozdil nekonecen je? :)
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#12 19. 01. 2009 23:50
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1853
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Limita
↑ gekoncik:
Nekonečno minus nekonečno je nedefinovaný výraz, stejně tak třeba nekonečno děleno nekonečno.
2+2=4
Offline
#14 20. 01. 2009 12:50
Re: Limita
Nevim ale ja to chapu tak ze co je konstata pred funkci muzes dat pred limitu a zatim mi to funguje a jedno jeslti je to exponent.. Ale muze to byt jen pravidlo limit v exponentu jak mas trebas scitani, podil atd.. Tady to mas na wiki http://cs.wikipedia.org/wiki/L'Hospitalovo_pravidlo
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#15 20. 01. 2009 13:39
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Limita
↑ Rohac:Důvod, proč 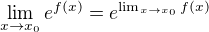 je ten, že funkce e^x je spojitá a pro spojitou funkci g platí, že pokud limita
je ten, že funkce e^x je spojitá a pro spojitou funkci g platí, že pokud limita 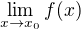 existuje, pak
existuje, pak 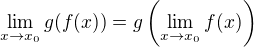 .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
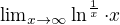 ?
?