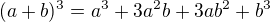Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 02. 11. 2013 23:09 Příspěvek uživatele Sherlock byl skryt uživatelem Aktivní. Důvod: wow
#7 02. 11. 2013 23:28
Re: rovnice o jedné neznámé
↑ bismarck:
tak po úpravě to už vychází těch 3,51. Díky moc. Jen by zajímalo jak jste na to došli... :)
Offline
 ? Vubec si nevím rady. h, ka a kp jsou konstanty.
? Vubec si nevím rady. h, ka a kp jsou konstanty.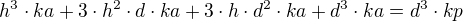

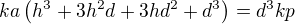
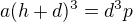
![kopírovat do textarea $(h+d)\sqrt[3]{a}=d\sqrt[3]{p}$](/mathtex/6d/6ddc3b354e46068e8f5e9ebd294cfec3.gif)
![kopírovat do textarea $d=\frac{h\sqrt[3]{a}}{\sqrt[3]{a}+\sqrt[3]{p}}$](/mathtex/29/293988e3b19c1bf1fd7d41f940734f08.gif) za předpokladu, že
za předpokladu, že 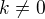
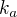 a
a 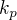 jsou konstanty - tam nemůžeš zkrátit
jsou konstanty - tam nemůžeš zkrátit 
![kopírovat do textarea $d=\frac{h\sqrt[3]{a}}{\sqrt[3]{p}-\sqrt[3]{a}}$](/mathtex/f7/f71b14e54e88a80457add868a88b025b.gif)
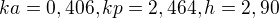 , tak
, tak 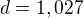 , ale výsledek by měl vyjít cca 3,52...
, ale výsledek by měl vyjít cca 3,52...