Matematické Fórum

Peta8 · 04. 11. 2013 18:54

Prosím, jde to vyřešit? Já na to nějak "nevidím".

$\sin(x)+\cos(x) = \frac{E}{8 } \\ \\ \tan(x)=?$

gadgetka

Nevím, zda jsem na to šla správně, ale vyšlo mi $(\text{tg}x)_{1,2}=\frac{-64\pm E\sqrt{128-E^2}}{64-E^2}$

Vyšla jsem z kladné hodnoty $\sin x=\frac{\text{tg}x}{\sqrt{1+\text{tg}^2x}}$ a stejně tak z hodnoty $\cos x =\frac{1}{\sqrt{1+\text{tg}^2x}}$

Našla jsem chybu, tak vzorec sedí se Zdeňkovým... krátila jsem čtyřmi pod odmocninou a nedala jsem to před odmocninu... njn...

zdenek1 · 04. 11. 2013 20:04

↑ Peta8:
Když to umocníš (a tady by se hodila nějaká podmínka na $E$ , jinak se bude muset dělat zkouška) dostaneš
$\sin ^2x+2\sin x\cos x+\cos ^2x=\frac{E^2}{64}$
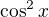$2\sin x\cos x=\frac{E^2-64}{64}$ nyní celou rovnici vydělíš $\cos^2x$ (můžeš, kosinus musí být kvůli tangensu různý od nuly)
$2\tan x=\frac{E^2-64}{64}\cdot \frac{1}{\cos ^2x}$
protože $\frac{1}{\cos ^2x}=1+\tan^2x$
máš
$2\tan x=(1+\tan^2x)\cdot \underbrace{\frac{E^2-64}{64}}_{k}$
což vede na rovnci
$k\tan^2x-2\tan x+k=0$
a ta má řešení
$\tan x=\frac{1\pm\sqrt{1-k^2}}{k}$
a nyní tam vrátíš ten zlomek
mě to po úpravách vyšlo
$\tan x=\frac{64\pm E\sqrt{128-E^2}}{E^2-64}$