Matematické Fórum

Pavel Brožek

Pro dané přirozené 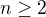$n\ge2$ si představme následující pokus:

Máme n očíslovaných mincí. Pomocí těchto mincí budeme tvořit n posloupností (každé minci přísluší jedna posloupnost) tak, že si vždy hodíme najednou všemi mincemi (to považujeme za jeden hod) a do příslušné posloupnosti si zapíšeme 0 nebo 1 podle toho, jestli na příslušné minci padla panna nebo orel. Ve chvíli, kdy žádné dvě posloupnosti nejsou shodné, skončíme, počet uskutečněných hodů označíme k.

Definujeme náhodnou veličinu X=k. Najděte střední hodnotu X v závislosti na n.

(Řešení neznám, ani nevím, jak je úloha obtížná.)

Edit: Zpřesněno zadání, aby bylo srozumitelnější

KennyMcCormick

EDIT: Takhle to nepůjde.

Co to zkusit takto:

Je to Narozeninový problém s následující modifikací:

Možností není 365, ale 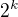$2^k$ .

Pravděpodobnost, že žádné 2 posloupnosti nebudou stejné právě při k-tém hodu, tedy bude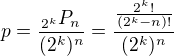
$p=\frac{_{2^k}P_n}{(2^k)^n}=\frac{\frac{2^k!}{(2^k-n)!}}{(2^k)^n}$ .

Náhodná veličina 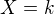$X=k$ má geometrické rozdělení.

Její střední hodnota bude
$E[X]=\frac1p=\frac1{\frac{\frac{2^k!}{(2^k-n)!}}{(2^k)^n}}=\frac{(2^k)^n}{\frac{2^k!}{(2^k-n)!}}=(2^k)^n\frac{(2^k-n)!}{2^k!}$ .

Pavel Brožek

↑ KennyMcCormick:

Ta pravděpodobnost p, kterou uvádíš, je pravděpodobnost, že dvě posloupnosti budou různé po k hodech. Nás ale hlavně zajímá, jaká je pravděpodobnost, že budou po k hodech poprvé různé (tj. po k-1 hodech ještě všechny různé nebyly).

Vůbec mi není jasné, proč myslíš, že X má geometrické rozdělení. A už vůbec mi není jasný ten výpočet střední hodnoty, vždyť ta nemůže záviset na k. Spočte se přece jako

$E[X]=\sum_{k=0}^\infty kp(k).$

KennyMcCormick · 05. 11. 2013 16:03

Máš pravdu, $X$ nemá geometrické rozdělení, protože $p$ je funkcí $k$ (takže ani $E[X]$ nebude takové, jaké jsem napsal).

Díky za upozornění na omyl.

check_drummer · 05. 11. 2013 20:40

↑ Pavel Brožek:
Ahoj, takže jestli to dobře chápu, tak po prvním hodu budeme mít vytvořen první člen každé posloupnosti, po druhém hodu budeme mít dva členy každé posloupnosti, atd.? A pokud se některé dvě takto doposud vytvořené posloupnosti shodují, tak pokračujeme v házení dále?

PS: Koukám, že jsi se dal na informatiku. Ve fyzice bylo tedy již vše objeveno a zbývá jen upřesnit hodnoty důležitých konstant? :-) (Abych citoval vážně míněné tvrzení někdy z konce 19. století.)

Pavel Brožek · 05. 11. 2013 20:49

↑ check_drummer:

Ahoj, chápeš to správně. :)

Ano, dal jsem se na informatiku :). Mám takový pocit, že abych se ve fyzice přiblížil něčemu významnému, tak bych jí musel prakticky obětovat život, což se mi nechce. A ani práce vědce mě zas tak moc neláká. V informatice má člověk mnohem víc možností uplatnění bych řekl.

check_drummer · 05. 11. 2013 20:58

↑ Pavel Brožek:
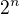Zkoušel jsi si to simulovat pro nějaké hodnoty n? Dolním odhadem je $log_2{n}$ a horním $2^n$ , tak by bylo zajmavé vidět, kde se ta střední hodnota pohybuje - třeba bude nakonec záviset na n lineárně (to by bylo velmi zajímavé).

Pavel Brožek · 05. 11. 2013 21:24

↑ check_drummer:

Simulovat jsem to nezkoušel. Došel jsem ke stejnému tvaru jako má KennyMcCormick (vůbec mě nenapadlo, že jde o narozeninový paradox, dospěl jsem k tomu jiným způsobem). Pravděpodobnost, že se skončí právě po k hodech je rovna rozdílu pravděpodobnosti, že se skončí po k hodech nebo dříve, a pravděpodobnosti, že se skončí po k-1 hodech nebo dříve. Ta pravděpodobnost, kterou uvedl KennymcCormick je pravděpodobnost, že se skončí po k hodech nebo dříve. Takže pravděpodobnost, že se skončí právě po k hodech je

$P(k)={2^k\choose n}\frac{n!}{2^{nk}}-{2^{k-1}\choose n}\frac{n!}{2^{n(k-1)}}.$

(Přitom beru ${a\choose b}=0$ , pokud b>a.)

Ta střední hodnota se dá upravit do tvaru

$E[x]&=a+\sum_{k=a}^\infty$1-{2^k\choose n}\frac{n!}{2^{nk}}$=\\ &=a+\sum_{k=a}^\infty$1-1\cdot\(1-\frac1{2^k}$\cdot$1-\frac2{2^k}$\cdot\ldots\cdot$1-\frac{n-1}{2^k}$\),$

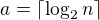kde $a=\lceil\log_2n\rceil$ . Členy sumy jsou zřejmě čísla z intervalu (0,1), takže dostáváme odhad $E[x]>\log_2n$ , který jsme očekávali. Ale bylo by zajímavé zjistit přesněji asymptotiku, tipnul bych si, že to bude nakonec právě ta logaritmická.

check_drummer · 06. 11. 2013 20:16

↑ Pavel Brožek:
Ahoj, to je vlastně pravda, že lze použít narozeninový paradox. Mohl bys prosím vysvětlit tu úpravu střední hodnoty - první řádek, kde je E[x]? Nezapomněl jsi násobit hodnotou k?
Možná by šel použít nějaký odhad na ten binomický koeficient a faktoriál pomocí čísla e. Nějaké odhady byly přímo na těch stránkách narozeninového paradoxu.

check_drummer · 06. 11. 2013 20:26

↑ Pavel Brožek:
Teď mě napadá, že tahle úloha souvisí s hashováním, o kterém jsi tu taky nedávno psal. Je to jen náhoda nebo jsi na tuto úlohu přišel v souvislosti se zkoumáním hashování?

Pavel Brožek

↑ check_drummer:

Je to trochu delší výpočet, než se k tomu člověk dostane. k mi tam nechybí, ono se v průběhu výpočtu ztratí samo :).

$E[x]&=\sum_{k=0}^\infty k${2^k\choose n}\frac{n!}{2^{nk}}-{2^{k-1}\choose n}\frac{n!}{2^{n(k-1)}}$=\\ &=\lim_{N\to\infty}\sum_{k=1}^N k${2^k\choose n}\frac{n!}{2^{nk}}-{2^{k-1}\choose n}\frac{n!}{2^{n(k-1)}}$=\\ &=\lim_{N\to\infty}$\sum_{k=1}^N k{2^k\choose n}\frac{n!}{2^{nk}}-\sum_{k=1}^Nk{2^{k-1}\choose n}\frac{n!}{2^{n(k-1)}}$=\\ &=\lim_{N\to\infty}$\sum_{k=1}^N k{2^k\choose n}\frac{n!}{2^{nk}}-\sum_{k=0}^{N-1}(k+1){2^{k}\choose n}\frac{n!}{2^{nk}}$=\\ &=\lim_{N\to\infty}$\sum_{k=a}^N k{2^k\choose n}\frac{n!}{2^{nk}}-\sum_{k=a}^{N-1}(k+1){2^{k}\choose n}\frac{n!}{2^{nk}}$=\\ &=\lim_{N\to\infty}$N{2^N\choose n}\frac{n!}{2^{nN}}+\sum_{k=a}^{N-1} (k-(k+1)){2^k\choose n}\frac{n!}{2^{nk}}$=\\ &=\lim_{N\to\infty}$N{2^N\choose n}\frac{n!}{2^{nN}}-N+N-\sum_{k=a}^{N-1}{2^k\choose n}\frac{n!}{2^{nk}}$=\\ &=\lim_{N\to\infty}$N{2^N\choose n}\frac{n!}{2^{nN}}-N$+\lim_{N\to\infty}$N-\sum_{k=a}^{N-1}{2^k\choose n}\frac{n!}{2^{nk}}$=\\ &=0+\lim_{N\to\infty}$a+N-a-\sum_{k=a}^{N-1}{2^k\choose n}\frac{n!}{2^{nk}}$=\\ &=a+\lim_{N\to\infty}\sum_{k=a}^{N-1}$1-{2^k\choose n}\frac{n!}{2^{nk}}$=\\ &=a+\sum_{k=a}^{\infty}$1-{2^k\choose n}\frac{n!}{2^{nk}}$$

Ve výpočtu jsem použil

$\lim_{N\to\infty}$N{2^N\choose n}\frac{n!}{2^{nN}}-N$&=0,$

nenapadá mě teď, jak důkaz této rovnosti stručně sepsat, a podrobně rozepisovat se mi to nechce, protože když si to člověk trochu rozepíše na papír, tak je to celkem zřejmé (dominantní člen se odečte a všechny ostatní klesají aspoň jako $\frac{N}{2^N}$ ).

Není to náhoda, souvisí to s hashováním. Konkrétně jsem na to narazil u Extendible hashing, kde je právě potřeba rozlišit každé dva hashe tím, že se budeme dívat na dostatečný počet bitů hashe. A zajímalo mě, jaký bude střední počet bitů, na které se musím dívat. Chtěl jsem tak při daném počtu záznamů zjistit, jak dobře v průměru bude využitý prostor adresáře.

check_drummer · 08. 11. 2013 20:51

↑ Pavel Brožek:
Děkuji za objsnění, čekal jsem že je to jen úprava na jeden řádek. :-)
Nad tou asymptotikou jsme se nezamýšlel, ale asi bude lepší aproximovat tu sumu (konečným součtem), co jsi odvodil, než to simulovat. I když u logaritmických závislostí je těch členů potřeba hodně. Viz třeba harmonická řada...

Matematické Fórum

#1 03. 11. 2013 19:43 — Editoval Pavel Brožek (05. 11. 2013 22:09)

Střední hodnota počtu pozic nutných pro rozlišení posloupností

#2 04. 11. 2013 23:52 — Editoval KennyMcCormick (05. 11. 2013 16:03)

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#3 05. 11. 2013 09:39 — Editoval Pavel Brožek (05. 11. 2013 12:53)

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#4 05. 11. 2013 16:03

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#5 05. 11. 2013 20:40

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#6 05. 11. 2013 20:49

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#7 05. 11. 2013 20:58

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#8 05. 11. 2013 21:24

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#9 06. 11. 2013 20:16

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#10 06. 11. 2013 20:26

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#11 06. 11. 2013 21:06 — Editoval Pavel Brožek (06. 11. 2013 23:31)

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

#12 08. 11. 2013 20:51

Re: Střední hodnota počtu pozic nutných pro rozlišení posloupností

Zápatí