Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kombinatorika na slovech (TOTO TÉMA JE VYŘEŠENÉ)
#3 07. 11. 2013 18:20 — Editoval Akcope (07. 11. 2013 20:51)
Re: Kombinatorika na slovech
↑ Rumburak:
Tak slov délky n celkově je určitě  .
.
Jak ale zjistit počet slov které tuto podmínku nesplňují?
Já na to koukal tímhle způsobem (možná je to skoro správně, prosím o kontrolu mé úvahy)
Do prvního chlívku lze určitě umístit 4 písmena. Pokud je první písmeno A nebo B, lze umístit do druhého chlívku jen 3 písmena. Pokud je C nebo D, lze tam umístit opět 4. A tak to pokračuje dále.
Takže jsem toto zprůměroval a řekl si, že výsledek by mohl být  . Zkoušel jsem to pro n = 2,3 a fungoval. Pro n = 1 tento vzorec nefunguje a pro n = 3 hodí desetinné číslo, takže je asi třeba něco doladit. Nevíte jestli je tohle správně, a pokud ano, jak tohle zobecnit?
. Zkoušel jsem to pro n = 2,3 a fungoval. Pro n = 1 tento vzorec nefunguje a pro n = 3 hodí desetinné číslo, takže je asi třeba něco doladit. Nevíte jestli je tohle správně, a pokud ano, jak tohle zobecnit?
Offline
#4 08. 11. 2013 11:51 — Editoval Rumburak (08. 11. 2013 11:57)
Re: Kombinatorika na slovech
Do prvního chlívku lze určitě umístit 4 písmena. Pokud je první písmeno A nebo B, lze umístit do druhého chlívku jen 3 písmena. Pokud je C nebo D, lze tam umístit opět 4. A tak to pokračuje dále.
To je, myslím, správná úvaha. Dejme jí nějakou formálnější podobu.
Nechť  je počet přípustných slov délky
je počet přípustných slov délky  , jejichž posledním znakem je
, jejichž posledním znakem je  .
.
Ptejme se, jak na tomto čísle závisí  , kde rovněž
, kde rovněž  . Musíme rozlišit několik případů:
. Musíme rozlišit několik případů:
I.  ... přípustné jsou
... přípustné jsou  , tedy 3 možnosti,
, tedy 3 možnosti,
II.  ... přípustné jsou
... přípustné jsou  , tedy 3 možnosti,
, tedy 3 možnosti,
III.  ... přípustné jsou
... přípustné jsou  , tedy 4 možnosti,
, tedy 4 možnosti,
IV.  ... přípustné jsou
... přípustné jsou  , tedy 4 možnosti.
, tedy 4 možnosti.
Odtud je také zřejmé, že
(1)  ,
,
protože možnost  se vyskytuje v případech I , III, IV , obdobně
se vyskytuje v případech I , III, IV , obdobně
(2)  ,
,
(3)  ,
,
(4)  .
.
Dále platí
(5)  ,
,  ,
,
protože prvek  má v úloze obdobné postavení jako prvek
má v úloze obdobné postavení jako prvek  a
a  má obdobné postavení jako
má obdobné postavení jako  ,
,
Je-li 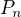 počet všech přípustných slov délky
počet všech přípustných slov délky  , potom
, potom
 .
.
Čísla  získáme řešením soustavy diferenčních rovnic
získáme řešením soustavy diferenčních rovnic
 ,
,

odvozené ze vztahů (1) , ... , (5). Počátečními podmínkami jsou zřejmě  .
.
Tak doufám, že tam nemám chybu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kombinatorika na slovech (TOTO TÉMA JE VYŘEŠENÉ)

 tak, aby a,b nikdy nesousedily?
tak, aby a,b nikdy nesousedily?