Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Prezentovaná úloha - posloupnosti. (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 11. 2013 21:36 — Editoval jelena (08. 11. 2013 19:07)
Prezentovaná úloha - posloupnosti.
Jelena: úloha je z předmětu Úlohy matematické olympiády a je určena k prezentaci jako splnění studijní povinnosti. Věřím, že především [i]podpoříte samostatnou snahu budoucí učitelky. Děkuji.[/i]
ahoj,
prosím, pomohl by mi někdo s touto úlohou? Nejlépe popsat celý postup řešení, abych to pochopila :) díky
Je dáno přirozené číslo n. Určete 2n + 1 za sebou jdoucích přirozených čísel, pro která platí:
součet druhých mocnin prvních n + 1 čísel se rovná součtu druhých mocnin posledních n
čísel.
Offline
- (téma jako vyřešené označil(a) teriberi)
#4 08. 11. 2013 10:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prezentovaná úloha - posloupnosti.
↑ teriberi:
Zdravím,
kolega ↑ BakyX: pracuje s úpravou levé strany  a používá vzorec
a používá vzorec  , potom seskupuje a vytýká. A to bych se kolegy chtěla zeptat, zda by bylo stejně použitelné, pokud bychom dokazovali, že
, potom seskupuje a vytýká. A to bych se kolegy chtěla zeptat, zda by bylo stejně použitelné, pokud bychom dokazovali, že 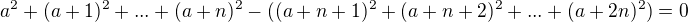 ? To bychom mohli používat
? To bychom mohli používat  pro "členy proti sobe"? Děkuji.
pro "členy proti sobe"? Děkuji.
↑ teriberi: co znamená "prezentované úlohy" (je to starší odkaz)? Děkuji.
Offline
#6 08. 11. 2013 19:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prezentovaná úloha - posloupnosti.
↑ teriberi:
kolega ↑ BakyX:, pokud bude mít zájem a čas, tak určitě pro Tebe bude více užitečný v diskusi. Samotnému zadání úlohy jsi rozuměla? Jaké máte materiály? Procházela jsi například návodné úlohy k olympiádě nebo materiály matematických seminářů?
Možným vodítkem by mohlo být jediné téma, které jsem kdy založila v sekci Zajímavých úloh (a to k obrazu Bogdanova-Belskoho) . Aktuálně v Opavě lze vidět obraz stejného autora (zde je pojmenován Svačina, ale na Internetu vidím názvy jako Svátek učitelky).
Upravím název tématu a přesunu do Zajímavých pro ZŠ, přeji úspěšnou debatu s kolegy.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Prezentovaná úloha - posloupnosti. (TOTO TÉMA JE VYŘEŠENÉ)


 ,
, 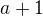 , ..
, ..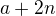 .
.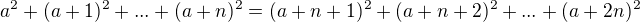 , takže
, takže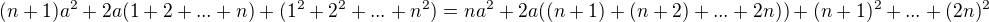


 , potom platí
, potom platí