Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 15. 11. 2013 21:48
Re: Exponenciální rovnice
Pomocí derivace se ukáže že funkce 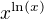 nabývá svého ostrého globálního minima v bodě
nabývá svého ostrého globálního minima v bodě  .
.
Dále jde vidět, že pro každé reálné  je
je  .
.
Z těchto dvou tvrzení hned plyne, že pro  platí
platí  .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 20. 11. 2013 11:07
Re: Exponenciální rovnice
↑ Keeeeke:
Jak už psal ↑ BakyX:, pomocí nerovností.
Rozmysli si, že pro  je
je  , stejně tak pro
, stejně tak pro  .
.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
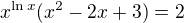
 a ihned vidíme, že jedním jejím kořenem je
a ihned vidíme, že jedním jejím kořenem je 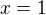 .
. 