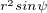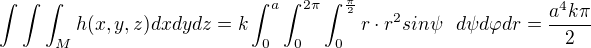Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » sfericke souřadnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 11. 2013 19:10 — Editoval Bodye (16. 11. 2013 19:59)
sfericke souřadnice
Zdravím, potřeboval bych trochu popostrčit při řešení tohodle příkladu:
Vypočítejte hmotnost a určete souřadnice těžiště polokoule kde hustota h(x,y,z) v danám bodě je přimo uměrná vzdálenosti od počátku. Polokoule ohraničená rovinou z=0 a plochou z=sqrt(a^2-x^2-y^2)
kde jsem se po převodu na sferické souřadnice dostal k tomuto a nevím jesli je to dobře.![kopírovat do textarea $\int_{0}^{a}\int_{0}^{2\pi}\int_{0}^{\frac{\pi }{2}} k[(rcos\varphi sin\\\psi )^{2}+(rsin\varphi sin\psi )^{2}+(rcos\psi )^{2}]^{\frac{1}{2}}r^{2}sin\psi d\psi d\varphi dr $](/mathtex/31/31d43d3502da3fae76775c5edb5c4cdb.gif)
hmotnost mi vysla :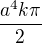
Offline
- (téma jako vyřešené označil(a) Bodye)
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » sfericke souřadnice (TOTO TÉMA JE VYŘEŠENÉ)