Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 11. 2013 21:12 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: téma je již otevřeno
#3 16. 11. 2013 23:14 — Editoval jelena (17. 11. 2013 10:38)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limity goniometrických funkcí
Téma jsem již otevřela,
zde je jedna z možností (poslat x v jmenovateli pod odmocninu - to nebude dobré, zapomene se na absolutní hodnotu) a opět rozšiřovat zlomek (pod odmocninou) ve stejném směru.
EDIT: nebudu posílat x pod odmocninu, jen rozšířím pod odmocninou zlomek 
Offline
#4 17. 11. 2013 00:24 — Editoval Freedy (17. 11. 2013 00:25)
Re: limity goniometrických funkcí
co třeba takhle? 



a=2b
:D vzhledem k tomu, že podle wolframu to tak nevyjde, navíc dokonce že ta limita ani neexistuje (oboustranná), tak si myslím že sem asi někde udělal chybu
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 17. 11. 2013 00:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limity goniometrických funkcí
↑ Freedy:
Zdravím,
řekla bych, že jsi trochu překombinoval (můžeš zůstat u 5x, potom poloviční je 2,5x), ale podstatnější bude, že odmocňuješ bez úvahy o znaménku sin zleva a zprava od 0.
Offline
#9 17. 11. 2013 10:32 Příspěvek uživatele Freedy byl skryt uživatelem Freedy. Důvod: duplicita příspěvku
#10 17. 11. 2013 10:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limity goniometrických funkcí
↑ ttt_:, ↑ Freedy:
Zdravím oba,
oba nemáte absolutní hodnotu ↑ příspěvek 5:, ale také jsem opravila svůj návrh o poslání x pod odmocninu, protože tak bych také zapomněla uvažovat různé znaménko sin(x) nalevo a napravo od 0. Zbytek o rozšíření platí.
↑ Freedy:
pořád si myslím, že více takových substituci vede ke zbytečnému přehlédnutí (a je až moc podezřele, jak hned pracuješ s  ) odkud jsi to uviděl hned na začátku úpravy? Děkuji.
) odkud jsi to uviděl hned na začátku úpravy? Děkuji.
Offline
#11 17. 11. 2013 10:48
Re: limity goniometrických funkcí
Pracuju s tím proto protože je tam cos(5x) = proto pětka
a protože chci mít dole odmocninu ze dvou, abych mohl použít vzorec:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#13 17. 11. 2013 10:53
Re: limity goniometrických funkcí
Tak dal sem tam nejdřív 20 jenže sem si neuvědomil že:
Nevidím na tom nic zázračného že mě to dopadlo. Samozřejmě že sinus je nalevo a napravo od nuly s rozdílným znaménkem, takže by to chtělo asi nějak ošetřit tou absolutní hodnotou. Ono ve výsledku vyjde 5odmocnin ze dvou / 2 jenže + a -. Takže ta absolutní hodnota by se tam asi hodila
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 17. 11. 2013 11:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limity goniometrických funkcí
↑ Freedy:
já na tom ani nic zázračného nevidím, jen mi to příliš připomíná výsledek z WA, tak to vypadá jako cílená cesta.
Absolutní hodnota je ze vzorce pro poloviční úhel (já při své úpravě také nesmím zapomenout na absolutní hodnotu, protože budu odmocňovat. ale moje původní úprava poslat x pod odmocninu by tento moment skryla z pozornosti, což není OK).
Existuje takový nástroj FMEA a ten říká, jak máme uvažovat příčiny a následky poruch (a opakuji - zde více substitucí je zdroj problémů). Ale horší zdroj je opomenutí absolutní hodnoty.
Offline
#15 17. 11. 2013 11:03
Re: limity goniometrických funkcí
Kdybych se na ten podíval nebo nepodíval, úvahu sem měl od začátku jasnou, použít vzorec na sin x/2. Jen si prostě myslím že 4 je odmocnina ze dvou a to je špatný.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#17 17. 11. 2013 11:44
Re: limity goniometrických funkcí
Poznamka: Najprv je trochu divine ze ↑ simushka8: nevyjadril nic o tom ako sa pokusil dostat k vysledku ...
Navrhuta metoda kolegamy pochopitelne vedie k vysledku, ak pouziju poznamky co im dala kolegina Jelena.
Inac trochu rychlejsia cesta k vysledku moze pouzit toto
No vsak ani tu sa nesme ignorovat , ze  pre kazde realne
pre kazde realne  ako to vyjadrila kolegina Jelena ( ktoru pozdravujem).
ako to vyjadrila kolegina Jelena ( ktoru pozdravujem).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 17. 11. 2013 12:16
Re: limity goniometrických funkcí
Ahoj ↑ jarrro:,
Odpadnu, lebo tvoj zapis vyuzil presne jej definiciu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 17. 11. 2013 12:39
Re: limity goniometrických funkcí
Alebo mozes argumentovat aj takto : akoze  preto
preto  ma to iste znamienko ako
ma to iste znamienko ako  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



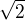 ? alebo ja to robim zle?
? alebo ja to robim zle?


