Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 11. 2013 16:54 — Editoval souteh (17. 11. 2013 16:56)
Limita posloupnosti
Zdravím, pomůže mi někdo s tímhle příkladem, prosím? Mám jich víc, budu pak přidávat další témata...
napadlo mě vytknout n a ve jmenovateli udělat "fígl" - místo n dát  , tím pádem bych ale dostal jako jednu část zlomku
, tím pádem bych ale dostal jako jednu část zlomku  a to je blbost.. tak prosím o nějaký funkčnější postup :)
a to je blbost.. tak prosím o nějaký funkčnější postup :)
Offline
- (téma jako vyřešené označil(a) souteh)
#4 17. 11. 2013 22:37 — Editoval bejf (17. 11. 2013 22:42)
Re: Limita posloupnosti
↑ souteh:
Určitě.
Teď to máš jakoby takovýto zlomek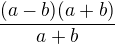 což je v podstatě
což je v podstatě  vidíš to tam?
vidíš to tam?
Tím, že se to umocní ten vršek nadruhou, tak se zbavíš těch odmocnin a vyjde:
Teď budem vytýkat nejvyšší mocninu.
Červená nka se zkrátí a zbyde: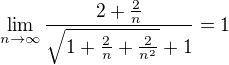
Offline

 zde rozšiř výrazem
zde rozšiř výrazem 
 a
a 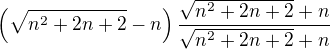 jsou dvě různé věci.
jsou dvě různé věci.