Matematické Fórum

bonifax

Do elipsy $x^2+3y^2=36$ vepište čtverec KLMN (tj. vrcholy K, L, M, N leží na elipse). Vypočítejte souřadnice vrcholů čtverce a jeho stranu.

$x^2+3y^2=36$
$3x^2+y^2=36$
--------------------------

$x=\pm 3$

Ahoj, můžu se zeptat, proč ta druhá elipsa " $3x^2+y^2=36$ " prochází krásně vrcholy čtverce.

Jak byste to obhájili. Děkuji předem, krásný večer přeji.)

bonifax · 04. 06. 2013 20:34

↑ marnes:

Ano, to vím, i tuto metodu přes osy kvadrantů jsem počítal. Mám vyřešený oba postupy.

Píšu seminární práci na téma "ELIPSA" rád bych nějak obhájil tento postup, proč tomu, tak je ale.

Proč ta elipsa s vertikální orientací přesně prochází těmi vrcholy..nějak matematicky odůvodnit to nevím..

bonifax

↑ marnes:

Nevím, co přesně hledat, ani nevím jak to souvisí s tím čtvercem.

marnes · 04. 06. 2013 21:22

↑ bonifax:

Tak je osová souměrnost, středová souměrnost, posunutí a otočení. A body čtverce splňují podmínku otočení, stejně jako ty čtyři body těch elips. Nic víc jsem tím nechtěl říct???
Samozřejmě mohu své náměty smazat, což taky udělám a třeba ti někdo odpoví jinak.

bonifax · 20. 11. 2013 21:25

Ahoj, omlouvám se, že otevírám znovu staré téma.

Vracím se zpět k původní otázce, pomohli mi někdo zodpovědět na otázku:

Proč ta druhá elipsa " $3x^2+y^2=36$ " prochází přesně vrcholy čtverce?

↑↑ marnes: - mám tedy uvést, že

Vrcholy čtverce prochází elipsou 3x^2+y^2=36 z toho důvodu, že zde platí osová souměrnost, středová souměrnost, posunutí a otočení? A tak by tomu bylo vždy? i v jiných případech?

marnes · 20. 11. 2013 22:55

↑ bonifax:

Vrcholy čtverce prochází elipsou 3x^2+y^2=36 z toho důvodu, že zde platí osová souměrnost, středová souměrnost, posunutí a otočení? A tak by tomu bylo vždy? i v jiných případech?

To jsem jen vyjmenoval možnosti zobrazení.

Pokud bych měl nějak odpovědět, tak za sebe tvrdím, že jak body čtverce KLMN, tak i body elipsy KLMN jsou otočeny o 90 stupňů ( jinak řečeno, že jen tyto body když otočím, tak budou opět ve vrcholech čtverce)
Nevím jak jinak to formulovat. Snad se někdo přidá a vytvoří lepší formulaci.

Honzc · 21. 11. 2013 07:40 — Editoval Honzc (21. 11. 2013 08:16)

↑ bonifax:
Já bych to vysvětlil takto:
1. Jedna z úhlopříček čtverce KLMN má rovnici (jako přímka) 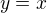$y=x$
2. Souřadnice jednoho z vrcholů se tedy spočítá jako řešení soustavy
$x^2+3y^2=36\\ y=x$
3. Protože 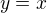$y=x$ , pak záměnou x za y dostaneme ten samý vrchol ležící na elipse $3x^2+y^2=36$

Nebo
1. Vezměme pouze čtvrtinu elipsy $x^{2}+3y^{2}=36$ (třeba takovou, kdy $x>0\wedge y>0$ , tj. aby to byla funkce)
2. Pak inverzní funkce vznikne záměnou x za y tedy její rovnice bude $y^{2}+3x^{2}=36$ ( $x>0\wedge y>0$ )
3. Jak známo inverzní funkce je osově souměrná s původní funkcí podle přímky 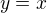$y=x$
4. Jejich půsečík (pokud existuje-a zde určitě existuje) nutně leží leží na této přímce a protože 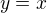$y=x$ je to vrchol čtverce
5. Protože elipsa se středem v počátku má osy souměrnosti y=0 a x=0 dostaneme další tři vrcholy vždy v některé z těchto souměrností.