Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 11. 2013 09:03
Důkaz nerovnosti
Dobrý den,
potýkám se s důkazem nerovnosti  pro
pro  Zkoušela jsem ten výraz různě upravovat, přesunovat z jedné strany na druhou, ale nic extra, co by mi pomohlo s důkazem, jsem v tom neviděla. :( Je vidět, že je všechno nezáporné a že funkce
Zkoušela jsem ten výraz různě upravovat, přesunovat z jedné strany na druhou, ale nic extra, co by mi pomohlo s důkazem, jsem v tom neviděla. :( Je vidět, že je všechno nezáporné a že funkce  je konvexní - napadlo mě nějak využít Jensenovu nerovnost, ale moc v tomhle případě nevím jak.. Prosím, mohli byste mě trochu popostrčit, jakým směrem se ubírat? Pomůže mi nějak rozvoj levé strany podle binomické věty?
je konvexní - napadlo mě nějak využít Jensenovu nerovnost, ale moc v tomhle případě nevím jak.. Prosím, mohli byste mě trochu popostrčit, jakým směrem se ubírat? Pomůže mi nějak rozvoj levé strany podle binomické věty?
Offline
- (téma jako vyřešené označil(a) nanny1)
#3 25. 11. 2013 10:38
Re: Důkaz nerovnosti
↑ Rumburak: Děkuju. Zatím nějak nemůžu přijít na to, jak se dospěje k té ekvivalentní úpravě, je to nějaký rozklad na parciální zlomky? Ještě mě napadá jedna možnost, pokud si teda správně myslím, že obecně platí  , ale je to tak jednoduchý, že to asi bude špatně. :D
, ale je to tak jednoduchý, že to asi bude špatně. :D
Offline
#6 25. 11. 2013 11:55 — Editoval nanny1 (25. 11. 2013 12:00)
Re: Důkaz nerovnosti
Už jsem to pochopila, teď ještě najít to minimum.. Nevím, jestli to mám dobře, vychází mi minimum v bodě x=0,5, pro který vychází rovnost s výrazem na levé straně  . Pro ostatní hodnoty x z intervalu <0,1> vychází na levé straně vždycky menší číslo. Tím pádem nerovnost platí. Jestli se nepletu..
. Pro ostatní hodnoty x z intervalu <0,1> vychází na levé straně vždycky menší číslo. Tím pádem nerovnost platí. Jestli se nepletu..
Offline

 je triviální.
je triviální.  ,
,  jsou nezáporná a splňují rovnici
jsou nezáporná a splňují rovnici  .
.  na intervalu
na intervalu  .
. , který je za příslušných předpokladů (včetně
, který je za příslušných předpokladů (včetně  ) kladný.
) kladný. pro uvažovaná
pro uvažovaná  obecně neplatí (viz případ
obecně neplatí (viz případ 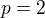 ).
).