Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 11. 2013 18:22
Binomická věta
Dokáže mi někdo dát lekci ve stylu "Binomická věta pro blbce"? Jak tak koukám na tu její definici, přesně něco takového bych totiž potřeboval.
Mám tady nějaké základní příklady.
Umocněte dvojčlen podle binomické věty:
1) 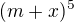
2) 
3) 
A nějaké slovní úlohy:
1) Určete koeficient 6. členu binomického rozvoje výrazu 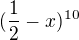
2) Určete jedenáctý člen binomického rozvoje výrazu 
I wish you best of luck...
Offline
#2 25. 11. 2013 19:05 — Editoval Oxyd (25. 11. 2013 19:06)
Re: Binomická věta
Binomická věta tedy říká, že  -- to jenom abychom si ustálili značení.
-- to jenom abychom si ustálili značení.
Tak pojďme řešit ten první příklad. Podle binomické věty je  . To jsem jenom dosadil do věty – n je 5, a je m a b je x. Tuším, že tě hlavně mate ten zápis pomocí
. To jsem jenom dosadil do věty – n je 5, a je m a b je x. Tuším, že tě hlavně mate ten zápis pomocí  – to je jenom kompaktně zapsaný součet – za znakem
– to je jenom kompaktně zapsaný součet – za znakem  se vyskytuje nějaký výraz, který obsahuje k – do toho budeme postupně dosazovat hodnoty k = 0, k = 1, ..., k = 5. Že budeme dosazovat hodnoty v tomhle rozsahu poznáš z toho, co je napsané pod a nad
se vyskytuje nějaký výraz, který obsahuje k – do toho budeme postupně dosazovat hodnoty k = 0, k = 1, ..., k = 5. Že budeme dosazovat hodnoty v tomhle rozsahu poznáš z toho, co je napsané pod a nad  . Všechny tyhle výrazy získané dosazením k = 0, ..., k = 5 se sečtou.
. Všechny tyhle výrazy získané dosazením k = 0, ..., k = 5 se sečtou.
Tedy dosazuju: .
.
A to je vlastně výsledek – tomuhle se rovná ta levá strana po roznásobení. Jestli chceš (nebo to po tobě chce učitel), můžeš to ještě upravit a spočítat hodnoty těch kombinačních čísel: .
.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#3 25. 11. 2013 19:05
Re: Binomická věta
↑ Ace:
Ahoj.
Jestli se nepletu, tak je to něco ve stylu:
Ostatní dva příklady jsou stejné, jenom s tím rozdílem, že:
2) 
3) 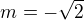
a bude se tam měnit znaménko podle toho jestli je to lichá nebo sudá mocnina.
Jistě si všimneš, že každý člen je uvozen kombinačním číslem.
Každý člen je uvozen  , kde postupně
, kde postupně 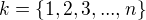 to znamená, že když máš rozvoj pátého řádu, tak
to znamená, že když máš rozvoj pátého řádu, tak 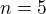 a těch členů bude
a těch členů bude  , takže v našem případě 6 celkem. První člen je uvozen
, takže v našem případě 6 celkem. První člen je uvozen  , druhý
, druhý 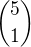 atd...z toho můžeš vyvodit nějaký pravidlo na zjištění koeficientu libovolného členu v libovolném rozvoji ne?
atd...z toho můžeš vyvodit nějaký pravidlo na zjištění koeficientu libovolného členu v libovolném rozvoji ne?
U těch dvou členů rozvoje se pak jen na střídačku mění exponenty...u prvního se začíná nejvyšší mocninou na kterou umocňuješ celý dvojčlen a u druhého naopak tou nejnižší a v rámci toho binomického rozvoje se u prvního mocnina snižuje o jedničku postupně a u druhého se postupně naopak zvyšuje o jedničku. Snad je to vidět.
Obecně na zjištění n-tého členu rozvoje existuje vzorec: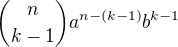
Offline
