Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 11. 2013 07:42
Re: -
↑ paha154:
Ahoj,
nedobře se na to díváš, Veverko. Účelem příkladů není napasovat zadání na nějaký vzorec, účelem je zamyslet se, pochopit zadání a pokusit se jej pomocí známých platných kroků vyřešit.
Tady konkrétně se na první pohled nabízí řešení hrubou silou, tedy napsat si program.
První nápad, která by tě mohl přivést k řešení (nebo k postupu, který už k řešení vede), je zamyslet se nad geometrickým "modelem". Rovnice:
popisuje rovinu v prostoru, která protíná souřadnicové osy v bodech [100,0,0], [0,100,0] a [0,0,100]. Ze zadání se můžeš omezit jen na kladný oktant bez bodů v rovinách daných osami. Teď si jen na rovině vymez body, pro které platí 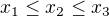 a zamysli se, jak zjistit počet bodů s celočíselnými souřadnicemi - jejich počet bude řešením tvého problému. Doporučuji si načrtnout pořádný obrázek - pokud mi to po ránu myslí, mělo by se jednat o trojúhelník s úhly 30-60-90 a s delší odvěsnou
a zamysli se, jak zjistit počet bodů s celočíselnými souřadnicemi - jejich počet bude řešením tvého problému. Doporučuji si načrtnout pořádný obrázek - pokud mi to po ránu myslí, mělo by se jednat o trojúhelník s úhly 30-60-90 a s delší odvěsnou 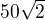 .
.
Доктор сказал «в морг» — значит в морг!
Offline
#3 27. 11. 2013 12:56
Re: -
↑ paha154:
Nebo se zkus zamyslet nad tímto:
Z podmínek úlohy plyne, že x může být pouze 0 a přirozené číslo menší rovno 33, to je celkem 34 možností.
Dále si zkus vzít x=33 a k tomu dle podmínek zjistit jaká y a z můžeš mít aby jejich součet byl 100.
Napovím:
x y z s počet součtů (možností)
33 33 34 100 1
32 32 36 100
32 33 35 100 3
32 34 34 100
31 31 38 100
31 32 37 100
31 33 36 100 4
31 34 35 100
30 30 40 100
30 31 39 100
30 32 38 100 6
30 33 37 100
30 34 36 100
30 35 35 100
atd.
Pro všechny součty tedy dostaneš řadu 1,3,4,6,7,9,10,12,....49,51 (celkem 34 členů)
To jsou dvě aritmetické posloupnosti, obě mají n=17 (členů) a d=3 (diference)
Teď už bys je mohl každou zvlášť sečíst a je hotovo.
Existuje ale ještě jedna finta, pro míň počítání
Zkus si sečíst vždy lichý a sudý člen, tedy 1+3=4,4+6=10,7+9=16,...,49+51=100
Teď je to opět aritmetická posloupnost, pro n=17,d=6,a1=4 a an=a17=100
A abys také něco udělal,tak na oba případy zkus použít vzoreček pro součet n členů aritmetické posloupnosti.
Offline
#4 28. 11. 2013 20:26 — Editoval paha154 (03. 12. 2013 14:43) Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#5 03. 12. 2013 21:25 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#6 04. 12. 2013 08:02 — Editoval Honzc (04. 12. 2013 10:18)
Re: -
↑ paha154:
Vysvětlení:
Protože součet má být 100, což je sudé číslo a z podmínkyx<=y<=z plyne, že u součtu 3 čísel, aby bylo sudé můžou být buď všechna 3 sudá, nebo 1 sudé a 2 lichá.
Tedy když začneme x=33 (liché číslo), pak y musí být liché číslo (33) a z sudé (34)
Pro x=32 (sudé) máme y=32 (sudé) a z=36 (sudé)
nebo y=33 (liché) a z=35 (liché)
nebo y=34 (sudé) a z=34 (sudé)
Tedy k možnosti pro x=33 přibyly 2 další. (celkem 3 možnosti)
Kdežto pro x=31 (liché) přibyde pouze jedna možnost y=31 (liché) z=38 (sudé) (celkem 4)
atd.
Pak tedy postupně přibydou 2,1,2,1,2..., což jsou dvě aritmetické posloupnosti s diferencí 3.
Podívej se na sloupečky v mém předchozím odkazu a sleduj sloupeček y a uvidíš, že pro klesající x přibyde řádek nahoře a dole (pro x sudé) a pouze řádek nahoře (pro x liché)
Offline
#7 05. 12. 2013 11:46 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#8 05. 12. 2013 12:48
Re: -
↑ paha154:
Dobře tak jinak.
Teď se pouze dívej vždy na sloupeček pod y (a neber jakoby ohled na x a z)
pro první možnost (x=33) může být y pouze (podmínky + součet) y=33
Teď přejdi k x=32 (sudé) (a sleduj sloupeček y)
y=33 je uprostřed těch tří možností
a přibylo y=32 do řádku nad řádek, kde je y=33
a také y=34 do pod řádek, kde je y=33
pro x= 31 (liché) (a opět sleduj sloupeček y)
budou tam řádky, kde y=32,33,34 - to je stejný počet jako pro x=32
ale přibyde pouze řádek s y=31 (tedy pouze jeden nahoru) - to je důsledek toho, že y<=z a toho, že součet musí být 100.
atd.
Pro x=30 si to odzkoušej sám.
Pak když se díváš na počty možností vidíš, že pro lichá x je počínaje x=33 1,4,7, ...
a pro sudá x (počínaje x=32) 3,6,9,..
To, že diference je u obou řad 3 je logické, protože 2+1=3, ale i 1+2=3
Offline
#9 05. 12. 2013 13:27 — Editoval Brano (05. 12. 2013 13:27)
Re: -
↑ paha154:
Honzc to dobre pise ale skusim to prepisat tak trochu inak, mozno toto sa ti lahsie pochopi, ale je to to iste.
Mas hladat pocet rieseni 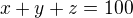 , pricom
, pricom 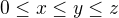 .
.
Urobme takuto substituciu 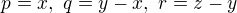 alebo teda
alebo teda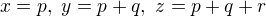 . Ked si to dosadime, tak hladame pocet rieseni
. Ked si to dosadime, tak hladame pocet rieseni , pricom
, pricom 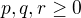 .
.
Riesenie si mozme napisat parametricky 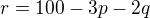 . To znamena, ze nech si zvolime lubovolne
. To znamena, ze nech si zvolime lubovolne  tak k nim najdeme (prave jedno)
tak k nim najdeme (prave jedno)  tak, ze mame riesenie a uz si len musime dat pozor, ze mozme volit iba nezaporne
tak, ze mame riesenie a uz si len musime dat pozor, ze mozme volit iba nezaporne  a iba tak, aby nam aj to
a iba tak, aby nam aj to  vyslo nezaporne.
vyslo nezaporne.
Ako teda mozme volit  ? No musi platit
? No musi platit 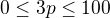 a teda
a teda 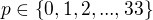 a potom k nemu volime
a potom k nemu volime  tak, aby
tak, aby 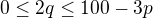 , cize
, cize .
.
To znamena, ze pre kazde mozne  (34 moznosti) mame
(34 moznosti) mame 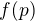 moznosti ako volit
moznosti ako volit  , kde
, kde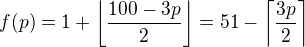 .
.
Vsimni si, ze ta postupnost 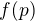 je presne ta co pise ↑ Honzc: len odzadu.
je presne ta co pise ↑ Honzc: len odzadu.
A teda vsetkych rieseni bude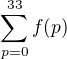 co je
co je
http://www.wolframalpha.com/input/?i=su … +n%3D0..33
tada .. 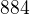 .
.
Offline
#10 05. 12. 2013 13:49 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#11 05. 12. 2013 13:58 — Editoval Brano (05. 12. 2013 13:59)
Re: -
↑ paha154:
mozme substituovat ako len chceme, ak je ta substitucia bijektivna (co je, lebo som vyjadril aj inverznu) a jej vyhoda je taka, ze to nie je len dobre definovana substitucia v 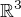 ale aj v
ale aj v 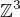 t.j. ze cele cisla prejdu na cele v oboch smeroch.
t.j. ze cele cisla prejdu na cele v oboch smeroch.
No a podstata je taka, ze pomerne hlupa sada nerovnosti 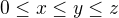 prejde na peknu sadu nerovnosti
prejde na peknu sadu nerovnosti 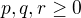 s ktorou sa lahko pracuje.
s ktorou sa lahko pracuje.
Offline
#12 05. 12. 2013 14:10 — Editoval Brano (05. 12. 2013 14:26)
Re: -
len este pre zaujemcov, taky trosku hlbsi vhlad do veci som nasiel tu:
http://math.stackexchange.com/questions … e-equation
Offline
