Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 11. 2013 22:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc s funkciou
Zdravím,
předpokládá se, že pro vyšetření funkce můžeš využívat diferenciální počet, nebo máš vycházet z vlastností funkce sinus? Děkuji.
Offline
#4 27. 11. 2013 23:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc s funkciou
↑ zzajabc:
tak budeme vycházet - jak jsi na tom transformaci grafu funkce? Předpokládám, že def. obor máš stanovený a teď budeš uvažovat, jak funkce  byla ovlivněna:
byla ovlivněna:
y=2sin(2x+1)+1, podařilo se odvodit jednotlivé změny funkce  ? Jelikož funkce je periodická, můžeme také stanovit periodu, na které vyšetřujeme, potom se chování funkce bude opakovat.
? Jelikož funkce je periodická, můžeme také stanovit periodu, na které vyšetřujeme, potom se chování funkce bude opakovat.
Co všechno už se podařilo? Děkuji.
Offline
#6 27. 11. 2013 23:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc s funkciou
↑ zzajabc:
děkuji, také mi tak vyšlo, jen u Hf je Hf=<-1,3>. Pro stanovení hodnot x, pro které funkce má min (max), stačí vyřešit rovnice:
2sin(2x+1)+1=-1 (pro min)
2sin(2x+1)+1=3 (pro max).
věřím, že ani intervaly monotonie nebude problém.
----------
:-) nemám problém ani s parnou/neparnou, ani se sudou/lichou.
Offline
#8 28. 11. 2013 12:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc s funkciou
↑ zzajabc:
jak vyšlo řešení rovnic ↑ příspěvek 6: ? Děkuji.
Offline
#10 28. 11. 2013 13:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc s funkciou
↑ zzajabc:
děkuji, také mi tak vyšlo. Pro základní interval si uspořádej hodnoty na ose x pro k=0 a k=1, potom se podaří zapsat základní intervaly monotonie.
Offline
#12 29. 11. 2013 00:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc s funkciou
Dosazeno dobře, ale není uspořádáno, pokud dobře vidím. Ještě upravím, aby bylo přehledněji výsledky předchozích příspěvků: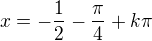 - lokalne min.
- lokalne min.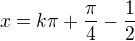 - lokal. max.
- lokal. max.
pro 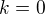 mame
mame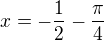 - lok. minimum je více nalevo od lokalního maxima pro k=0.
- lok. minimum je více nalevo od lokalního maxima pro k=0.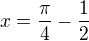 , funkce roste na intervalu
, funkce roste na intervalu 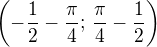 , potom do bodu dalšího minima pro
, potom do bodu dalšího minima pro 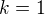 (což je
(což je 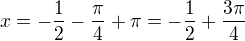 ) klesá.
) klesá.
Podívej se, pořádně, zda do intervalu monotonie zahrnujete i body extrému (tedy závorky jsou <...>) а jak budou zapsány intervaly pro periodické funkce. Jelikož pokud máte stejný zdroj zadání, tak to abych stala v pozoru u klávesnice a dávala si záležet na každé čárce, tak stejně budu mít hrůzu předložit vzácnému kolegovi k posudku :-) A právem.
Offline
