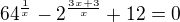Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 11. 2013 10:00
- lukasstork

- Příspěvky: 57
- Reputace: 0
Rovnice s mocninama a odmocninama
Ahoj potreboval bych pomoc s temihle rovnicemi moc vám Děkuju ![kopírovat do textarea $\sqrt[X]{64}-\sqrt[X]{2^{3x+3}}+12=0-------
16\cdot \sqrt{0,25^{5-x/4}}=2
$](/mathtex/f3/f3eadd0297f236819555c88edb8fbc56.gif)
Offline
#4 30. 11. 2013 10:17
Re: Rovnice s mocninama a odmocninama
↑ lukasstork:![kopírovat do textarea $\sqrt[x]{8^2}-\sqrt[x]{8^x}\cdot\underbrace{\sqrt[x]{8}}_{t}+12=0$](/mathtex/f8/f87118e28b5c12d211a05b868f30012c.gif)
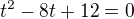
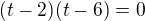
![kopírovat do textarea $\sqrt[x]{8}=2$](/mathtex/61/619445aa6f253459fe895afe8f28d617.gif) nebo
nebo ![kopírovat do textarea $\sqrt[x]{8}=6$](/mathtex/8e/8e1d3f0d0d29a4b118391faeaba91bbb.gif)
 nebo
nebo 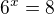
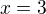 nebo
nebo 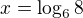
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 30. 11. 2013 10:21
Re: Rovnice s mocninama a odmocninama
↑ lukasstork: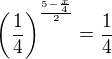
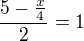
dopočítat
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 30. 11. 2013 10:49
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: Rovnice s mocninama a odmocninama
Ahoj promiň u ty 2 ma bejt 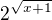
Offline
#7 30. 11. 2013 10:57
- janca361

- .
- Příspěvky: 3284
Re: Rovnice s mocninama a odmocninama
↑ lukasstork: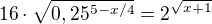
Takto nebo jinak?
Offline
#9 30. 11. 2013 11:03
Re: Rovnice s mocninama a odmocninama
↑ lukasstork: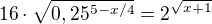
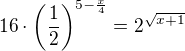
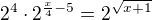
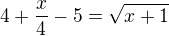
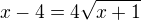
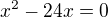
kořen  nevyhovuje
nevyhovuje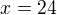
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 30. 11. 2013 11:17 Příspěvek uživatele janca361 byl skryt uživatelem janca361.
#11 30. 11. 2013 11:33
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: Rovnice s mocninama a odmocninama
Díky moc↑ zdenek1:
Offline
 má znamenat co?
má znamenat co?![kopírovat do textarea $\sqrt[X]{64}-\sqrt[X]{2^{3x+3}}+12=0$](/mathtex/6d/6d408b8eb1a946b59a1428ac7b3e6a55.gif)