Matematické Fórum

Dobrý den,
nevím si rady s příkladem 2 v projektu číslo 7
http://homel.vsb.cz/~kov16/files/dim2013_projekt07.pdf
Řekl bych že je relace reflexivní, neboť to plyne ze zadání.
Ostatními vlastnostmi už si však tak jistý nejsem. Na cvičení jsme probírali a vlastně skoro všude jsem našel jen jednoduché příklady typu a je v relaci s b, pokud platí, že a je starší než b, což chápu. Zde mi však dělá problém, že jsou relace dvě. Proto nevím zdali postupuji dobře. Zkusil jsem to takhle:
Relace je antisymetrická - zde jsem použil alternativní definici antisymetrie.
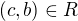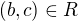Relace není tranzitivní - muselo by totiž platit, že jestliže a , pak 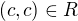, což zde neplatí, protože dvě černé políčka spolu nemohou být v relaci. (kde c je černá a b je bílá)
U určení symetrie však nevím jak postupovat, protože když se zaměřím na jedno konkrétní bílé a černé políčko, tak mi to připadá divné:
Relace není symetrická - pokud by bylo černé políčko napravo pod bílým tak nemůže být bílé políčko nalevo pod černým.
Předem děkuji za případné rady.