Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Projekt cislo 5 - uloha 5.4 b (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 11. 2013 12:51
Projekt cislo 5 - uloha 5.4 b
Dobry den, potreboval bych trochu poradit s touhle ulohou
Co je hamiltonovský graf?
Kolik různých hamiltonovských cyklů má kompletní graf 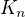 ?
?
Dva hamiltonovské cykly považujeme za stejné, procházejí-li stejnými vrcholy ve stejném pořadí. Tj. cyklus 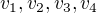 považujeme za stejný jako cyklus
považujeme za stejný jako cyklus 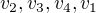 , ale různý od cyklů
, ale různý od cyklů 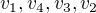
(je opačně orientovaný) a 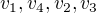 (má prohozené pořadí vrcholů).
(má prohozené pořadí vrcholů).
odpoved na 1. otazku: Graf, ve kterém existuje \textit{hamiltonovský cyklus}, se nazývá hamiltonovský graf
Odpoved 2:
Jesli jsem to pochopil tak na grafu 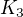 je tech cyklu muze byt 2
je tech cyklu muze byt 2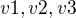 ,
, 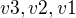
Takze na grafu 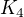 jich bude kolik?
jich bude kolik?
protoze mezi vrcholy 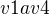 jsou 4
jsou 4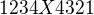
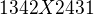
z tohoto se da uvazovat ze mezi libovolnymi 2 vrcholy budou 4 hamiltonovske cykly
Da se rict ze na  vrcholech bude
vrcholech bude 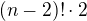 ,
, 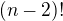 protoze muzu vychazet z jakeho koli bodu daneho cyklu a
protoze muzu vychazet z jakeho koli bodu daneho cyklu a  protoze cyklus v opacnem poradi je jiny?
protoze cyklus v opacnem poradi je jiny?
Offline
- (téma jako vyřešené označil(a) byk7)
#3 28. 11. 2013 17:32 — Editoval oglop (29. 11. 2013 14:02)
Re: Projekt cislo 5 - uloha 5.4 b
petrkovar napsal(a):
↑ oglop:K odpovědi 1. a co je to ten hamiltonovský cyklus?
K odpověd 2: A co cyklus?
hamiltonovský cyklus je cyklus ktery projde vsemi vrcholy prave jednou - to tam jeste dopisu, at tam mam tedy vsechny detaily
cyklu  jsem si nevsiml,
jsem si nevsiml,
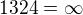
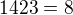
jsou 3 cykly 1 smerem
... zmenil jsem pristup uplne, musim si to promyslet aby to slo rozumne napsat.
co takhle?
Hamiltonovsky cyklus na  vrcholech je posloupnost
vrcholech je posloupnost  cisel, ja tedy je muzu seradit
cisel, ja tedy je muzu seradit  zpusoby, tim se mi tam zapociaji i cykly zacinajici na jednom z vrcholu, ktery uz v danem cyklu je.
zpusoby, tim se mi tam zapociaji i cykly zacinajici na jednom z vrcholu, ktery uz v danem cyklu je.
Takze musim dostat pryc vrcholy, ktere ten cyklus uz obsahuje. To bych mohl udelat tak ze
pocet moznosti v 1 cyklu vydelim poctem vrcholu v nem obsazenych.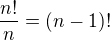 a to je pocet vsech hamiltonovskych cyklu na grafu
a to je pocet vsech hamiltonovskych cyklu na grafu 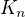 .
.
Offline
#5 30. 11. 2013 22:06
Re: Projekt cislo 5 - uloha 5.4 b
↑ petrkovar:
Já už to s ním dořešil. :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#8 03. 12. 2013 00:54
Re: Projekt cislo 5 - uloha 5.4 b
↑ petrkovar:
No mně nééé... :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Projekt cislo 5 - uloha 5.4 b (TOTO TÉMA JE VYŘEŠENÉ)
