Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » BP - mocninové rady (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 12. 2013 19:57
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
BP - mocninové rady
Ahojte,
píšem bakalárku na tému Mocninové rady a ich využitie. Hlavnou náplňou mojej práce sú dôkazy a teoretické veci, ktoré naformulujem podľa knihy od Rudina - Principles of mathematical analysis. Čo sa týka využitia v praxi, moc nápadov nemám. Vedeli by ste mi poradiť nejaký zdroj, či už knihu (aspoň bude dôvod konečne navštíviť knižnicu na matfyze :D) alebo článok na internete?
Vopred vďaka za každú radu.
Offline
- (téma jako vyřešené označil(a) Blackflower)
#2 04. 12. 2013 02:02 — Editoval Brano (04. 12. 2013 02:15)
Re: BP - mocninové rady
Kedze knihu az tak nepoznam, tak neviem, ze ci to co sa mne zda ako dolezite vyuzitie nie je nahodou pokryte uz tam, ale mne sa teda pacia nasledovne:
dolezite vyuzitie cislo 1) definicia funkcie  (rovno aj pre komplexne cisla)
(rovno aj pre komplexne cisla)
vyuzitie cislo 2) riesenie (niektorych) diferencialnych rovnic
a rovno ako priklad sa da uviest:
Riesme rovnicu  z teorie vieme, ze ma prave jedno riesenie.
z teorie vieme, ze ma prave jedno riesenie.
Co keby bolo analyticke? Potom by sa dalo napisat  co mozme dosadit.
co mozme dosadit.
teda  co sa vyriesi lahko
co sa vyriesi lahko
a z teorie o mocninovych radoch vieme, ze funkcia je dobre definovana pre lubovolne
je dobre definovana pre lubovolne 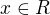 resp
resp 
a pomenujeme ju  a to je urcite (to jedine) riesenie nasej rovnice. neskor nahliadneme ako suvisi s umocnovanim.
a to je urcite (to jedine) riesenie nasej rovnice. neskor nahliadneme ako suvisi s umocnovanim.
Offline
#3 04. 12. 2013 04:39
Re: BP - mocninové rady
Ahoj ↑ Blackflower:,
Mozes presnejsie napisat co planujes dat do tvojej praci.
Tu mas mozny plan.
Napr. Je dobre zacat zo studium formalnej mocninovej rady. ( podobne ako sa studuju formalne polynomy ).
Potom mozes hovorit o polomere konvergencie ako aj o roznych druhoch konvergencii.
Tiez ako to funguje z limitamy. ...
Ako sa daju definovat funkcie z mocninovymi radamy.
A opacne kedy a ako mozeme najst pre danu funkciu jej mocninovu radu.
Ake operacie mozme robit z mocninovymi radami. ( napr derivaciu, integraciu, pouzitie funkcionalnych relacii... )
Suvis z aproximaciou funkcii ako Weirsrass-ova veta...
Suvis z realnymi analytickymi funkciamy.
Alebo aj z Dirichlet-ovymi radamy
Atd.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 04. 12. 2013 13:26 — Editoval vanok (04. 12. 2013 13:34)
Re: BP - mocninové rady
UAhoj,
Dnesna myslienka.
Prebehol som Rudin-ovu knihu.
Je to velmi dobra uvodna kniha do analyzy.
Co sa tyka Power Series, najdes tam len zakladne vlasnosti.
Plan co som ti navrhol ide o mnoho dalej, a odpoveda na vela otazok na ktore vela studentov nevie odpovedat.
V inej slavnej Rudinovej knihe: real and complex analysis, najdes v uvode zavedenie exp, co je jedna klasicka funkcia definovana vdaka takymto radom. (↑ Brano: o tom trochu pise).
Problem formalnych mocninovych radov je uvedeny napr tu http://en.wikipedia.org/wiki/Formal_power_series, (je to velmi uzitocne a zjednodusi znacne aj ine neskorsie vysledky)
Na pokracvanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 04. 12. 2013 20:48 — Editoval Blackflower (04. 12. 2013 20:49)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: BP - mocninové rady
↑ Brano: ↑ vanok: Čaute,
vďaka za reakcie. Moja školiteľka má o bakalárke v podstate presnú predstavu - mojou úlohou bude spracovať a "poľudštiť" teóriu plus vypočítať zopár príkladov (to ale neznamená, že nie som otvorená ničomu inému). Niečo k využitiu som si našla, diferenciálne rovnice plánujem spomenúť, aj keď sme ich ešte nemali, ale základné pojmy si nájdem a pokiaľ budem schopná to pochopiť, rozpíšem sa o tom viac (aj podľa počtu strán :D).
Možno sa ešte ozvem :D
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » BP - mocninové rady (TOTO TÉMA JE VYŘEŠENÉ)
